giải được tuicho 5 tỉ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
2 tháng 8 2021
Lời giải:
Theo như đề thì hàm lợi nhuận (y) và sản lượng (x) sẽ có dạng này:
Hàm lợi nhuận có dạng pt như sau:
$y=ax^2+bx+c$
Sản lượng bằng $0$ thì lợi nhuận đương nhiên bằng $0$
$\Rightarrow c=0$
ĐTHS đổi dấu tại $x=10$, tức là $x=10$ là điểm cực trị
$\Rightarrow \frac{b}{-2a}=10\Leftrightarrow b=-20a$
$y=ax^2-20ax$. Thay $x=5; y=170$ thì $a=-\frac{34}{15}$
Vậy hàm lợi nhuận là: $y=\frac{-34}{15}x^2+\frac{136}{3}x$
Tại $x=12$ thì $y=217,6$
Hàm lợi nhuận giảm với tốc độ là \(|y'(12).\frac{12}{217,6}|=0,5\) (%)
Vậy tại mức sản phẩm 12, khi mức sản phẩm tăng 1% thì lợi nhuận giảm 0,5 %.
LT
2
NM
2
CM
13 tháng 2 2018
Đáp án D
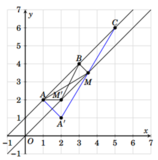
Cách 1
· Đặt 
biểu diễn cho số phức z.
· Từ giả thiết, ta có M thuộc đường trung trực 
của đoạn EF và P=AM+BM+CM
· Ta chứng minh điểm M chính là hình chiếu vuông góc của B lên đường thẳng ∆ .
- Với M’ tùy ý thuộc ∆ , M’ khác M. Gọi A’ là điểm đối xứng của A qua ∆ . Nhận thấy rằng ba điểm A’, M, C thẳng hàng.
- Ta có 
Mà 
Lại có 
Do đó 
Cách 2
· Gọi 
Từ giả thiết 
, dẫn đến y=x .
Khi đó z=x+xi.
· 
· Sử dụng bất đẳng thức 
Dấu đẳng thức xảy ra khi và chỉ khi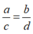 
. Ta có
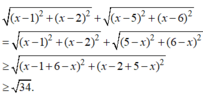
Dấu đẳng thức xảy ra khi và chỉ khi 
· Mặt khác
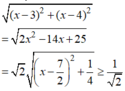
Dấu đẳng thức xảy ra khi và chỉ khi x= 7 2
· Từ hai trường hợp trên, ta thấy, giá trị nhỏ nhất của P là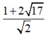 
.
Khi đó a+b=3.
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 2 2020
\(\frac{1}{1+tanx}=\frac{cosx}{cosx+sinx}=\frac{1}{2}\left(\frac{cosx+sinx}{cosx+sinx}+\frac{-sinx+cosx}{cosx+sinx}\right)\)
\(\Rightarrow\int\limits^{\frac{\pi}{4}}_0\frac{1}{1+tanx}dx=\frac{1}{2}\int\limits^{\frac{\pi}{4}}_0\left(1+\frac{-sinx+cosx}{cosx+sinx}\right)dx=\int\limits^{\frac{\pi}{4}}_0\frac{1}{2}dx+\frac{1}{2}\int\limits^{\frac{\pi}{4}}_0\frac{d\left(cosx+sinx\right)}{cosx+sinx}\)
\(=\frac{1}{2}x|^{\frac{\pi}{4}}_0+\frac{1}{2}ln\left(sinx+cosx\right)|^{\frac{\pi}{4}}_0=\frac{\pi}{8}+\frac{1}{2}ln\sqrt{2}=\frac{\pi}{8}+\frac{1}{4}ln2\)
\(\Rightarrow a=\frac{1}{8}\) ; \(b=\frac{1}{4}\)
\(\hept{\begin{cases}\text{a = 1}\\\text{b = 2}\\\text{c = 3}\end{cases}}\)
=> abc = 1 x 2 x 3 = 6 ( còn abc = 123 )
# Maths
abc = 123
HT