K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
N
9 tháng 3 2022
d) \(x+\dfrac{3}{4}=\dfrac{36}{144}.\dfrac{-12}{9}\)
\(\Rightarrow x+\dfrac{3}{4}=\dfrac{-1}{3}\)
\(\Rightarrow x=\dfrac{-1}{3}-\dfrac{3}{4}\)
\(\Rightarrow x=\dfrac{-4}{12}-\dfrac{9}{12}\)
\(\Rightarrow x=\dfrac{-13}{12}\)
e)
\(\dfrac{8}{23}.\dfrac{46}{24}=\dfrac{1}{3}.x\)
\(\Rightarrow\dfrac{1}{3}.x=\dfrac{2}{3}\)
\(\Rightarrow x=\dfrac{2}{3}:\dfrac{1}{3}\)
\(\Rightarrow x=\dfrac{2}{3}.3\)
\(\Rightarrow x=2\)
f)
\(\dfrac{1}{5}:x=\dfrac{1}{5}-\dfrac{1}{7}\)
\(\dfrac{1}{5}:x=\dfrac{7}{35}-\dfrac{5}{35}\)
\(\dfrac{1}{5}:x=\dfrac{2}{35}\)
\(\Rightarrow x=\dfrac{1}{5}:\dfrac{2}{35}\)
\(\Rightarrow x=\dfrac{1}{5}.\dfrac{35}{2}\)
\(\Rightarrow x=\dfrac{7}{2}\)
9 tháng 3 2022
g: \(\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2=\dfrac{4}{9}-\dfrac{1}{3}=\dfrac{1}{9}\)
=>x-1/2=1/3 hoặc x-1/2=-1/3
=>x=5/6 hoặc x=-1/6
h: \(\Leftrightarrow x\cdot\dfrac{16}{5}-\dfrac{22}{15}:\dfrac{11}{3}=\dfrac{7}{20}\)
\(\Leftrightarrow x\cdot\dfrac{16}{5}=\dfrac{7}{20}+\dfrac{22}{15}\cdot\dfrac{3}{11}=\dfrac{7}{20}+\dfrac{2}{5}=\dfrac{3}{4}\)
hay x=15/64
i: \(\Leftrightarrow\left(\dfrac{9}{2}-2x\right)=\dfrac{13}{2}:\dfrac{65}{61}=\dfrac{61}{10}\)
=>2x=-8/5
hay x=-4/5
8 tháng 3 2022
a: \(=\dfrac{2}{7}\cdot\dfrac{-3}{4}\cdot\dfrac{4}{7}=\dfrac{-6}{49}\)
b: \(=\dfrac{3}{5}:\dfrac{1}{15}=\dfrac{3}{5}\cdot15=9\)
c: \(=\dfrac{41}{7}-3-\dfrac{1}{2}=\dfrac{33}{14}\)
d: \(=-\dfrac{25}{12}-\dfrac{23}{12}-\dfrac{3}{2}=-4-\dfrac{3}{2}=-\dfrac{11}{2}\)
26 tháng 4 2021
TRẢ LỜI:
Đáp án: C
Trong hiện tượng giao thoa sóng trên mặt nước, khoảng cách giữa hai cực đại liên tiếp nằm trên đường nối tâm hai sóng có độ dài là một nửa bước sóng.
NB
1
6 tháng 3 2022
\(I=\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2009.2010}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2019}-\dfrac{1}{2010}\\ =1-\dfrac{1}{2010}\\ =\dfrac{2009}{2010}\)
\(K=\dfrac{4}{2.4}+\dfrac{4}{4.6}+...+\dfrac{4}{2008.2010}\\ =2\left(\dfrac{2}{2.4}+\dfrac{2}{4.6}+...+\dfrac{2}{2008.2010}\right)\\ =2\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{2008}-\dfrac{1}{2010}\right)\\ =2\left(\dfrac{1}{2}-\dfrac{1}{2010}\right)\\ =2.\dfrac{502}{1005}\\ =\dfrac{1004}{1005}\)
\(F=\dfrac{1}{18}+\dfrac{1}{54}+...+\dfrac{1}{990}\\ =\dfrac{1}{3.6}+\dfrac{1}{6.9}+...+\dfrac{1}{30.33}\\ =\dfrac{1}{3}\left(\dfrac{3}{3.6}+\dfrac{3}{6.9}+...+\dfrac{3}{30.33}\right)\\ =\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{9}+...+\dfrac{1}{30}-\dfrac{1}{33}\right)\\ =\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{33}\right)\\ =\dfrac{1}{3}.\dfrac{10}{33}\\ =\dfrac{10}{99}\)
6 tháng 3 2022
\(I=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2009}-\dfrac{1}{2010}=\dfrac{2010-1}{2010}=\dfrac{2008}{2010}\)
\(K=\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{2008}-\dfrac{1}{2010}=\dfrac{502}{1005}\)
\(F=\dfrac{1}{3.6}+\dfrac{1}{6.9}+...+\dfrac{1}{99.100}=\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{9}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)=\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{100}\right)=\dfrac{97}{900}\)
LT
13 tháng 3 2020
Những số có chữ số tận cùng là 2,4,8 khi nâng lên mũ 4 có tận cùng là 6
Thật vậy
\(4^{2k}=2^{4k}=...6\)
\(4^{2k+1}=2^{4k+2}=2^{4k}.4=\left(...6\right).4=...4\)
VB
2
23 tháng 12 2021
2021+(-247)+(-53)-2021=(2021-2021)+[(-247)+(-53)]
=0+(-300)
=-300
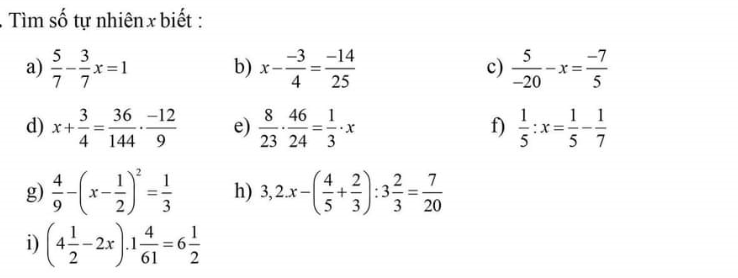
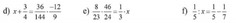
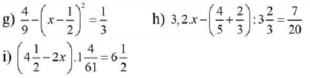
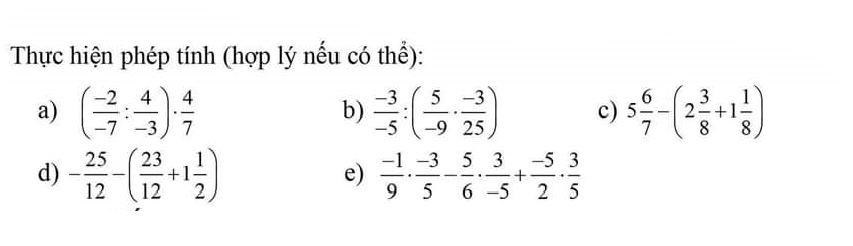
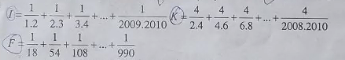
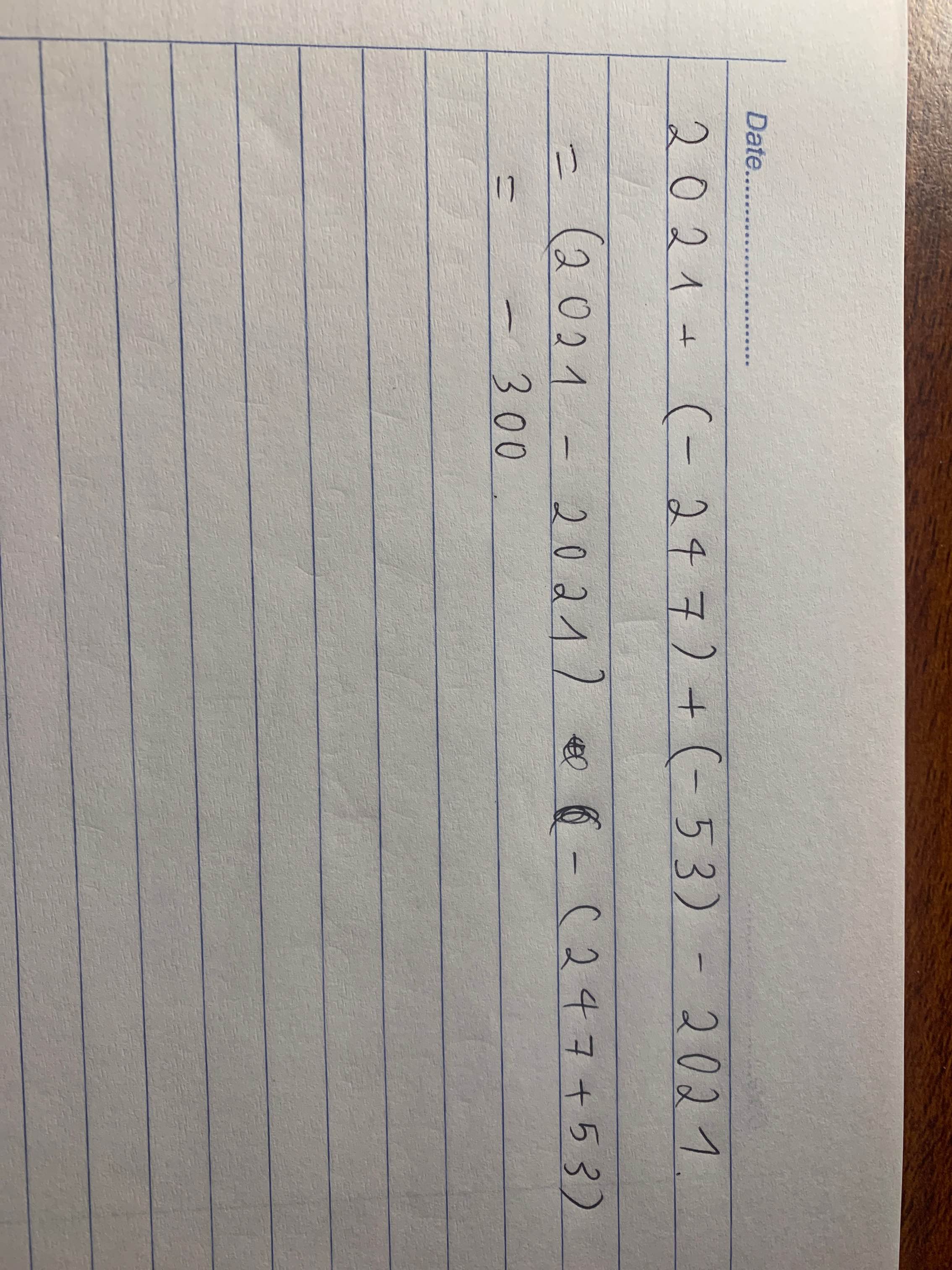
a: =>3/7x=5/7-1=-2/7
hay x=-2/3
b: =>x+3/4=14/25
=>x=14/25-3/4=-19/100
c: =>-1/4-x=-7/5
=>x+1/4=7/5
hay x=7/5-1/4=23/20