PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
18 tháng 4 2019
a) 4 x 4 + x 2 − 5 = 0
Đặt x 2 = t (t ≥ 0). Phương trình trở thành:
4 t 2 + t − 5 = 0
Nhận thấy phương trình có dạng a + b + c = 0 nên phương trình có nghiệm
t 1 = 1 ; t 2 = ( − 5 ) / 4
Do t ≥ 0 nên t = 1 thỏa mãn điều kiện
Với t = 1, ta có: x 2 = 1 ⇔ x = ± 1
Vậy phương trình có 2 nghiệm x 1 = 1 ; x 2 = − 1
b) 3 x 4 + 4 x 2 + 1 = 0
Đặt x 2 = t ( t ≥ 0 ) . Phương trình trở thành:
3 t 2 + 4 t + 1 = 0
Nhận thấy phương trình có dạng a - b + c = 0 nên phương trình có nghiệm
t 1 = - 1 ; t 2 = ( - 1 ) / 3
Cả 2 nghiệm của phương trình đều không thỏa mãn điều kiện t ≥ 0
Vậy phương trình đã cho vô nghiệm.
PT
1
CM
9 tháng 7 2017
Đặt m = x 2 .Điều kiện m ≥ 0
Ta có: x 4 -8 x 2 – 9 =0 ⇔ m 2 -8m -9 =0
Phương trình m 2 - 8m - 9 = 0 có hệ số a = 1,b = -8,c = -9 nên có dạng a – b + c = 0
suy ra: m 1 = -1 (loại) , m 2 = -(-9)/1 =9
Ta có: x 2 =9 ⇒ x= ± 3
Vậy phương trình đã cho có 2 nghiệm : x 1 =3 ; x 2 =-3
PT
1
CM
29 tháng 8 2019
Ta có: 3 x 4 – 6 x 2 = 0 ⇔ 3 x 2 ( x 2 – 2) = 0
Vậy phương trình đã cho có 3 nghiệm: x 1 = 0; x 2 = -√2 ; x 3 = √2
PT
1
PT
1
CM
24 tháng 4 2018
Ta có: 5 x 4 – 7 x 2 – 2 = 3 x 4 – 10 x 2 – 3
⇔ 5 x 4 – 7 x 2 – 2 – 3 x 4 + 10 x 2 + 3 = 0
⇔ 2 x 4 + 3 x 2 + 1 = 0
Đặt m = x 2 . Điều kiện m ≥ 0
Ta có: 2 x 4 + 3 x 2 + 1 = 0 ⇔ 2 m 2 + 3m + 1 = 0
Phương trình 2 m 2 + 3m + 1 = 0 có hệ số a = 2, b = 3, c = 1 nên có dạng :
a – b + c = 0 suy ra m 1 = -1, m 2 = -1/2
Cả hai giá trị của m đều nhỏ hơn 0 nên không thỏa mãn điều kiện bài toán.
Vậy phương trình vô nghiệm.
PT
1
CM
17 tháng 10 2019
Ta có: 2 x 4 + x 2 – 3 = x 4 + 6 x 2 + 3
⇔ 2 x 4 + x 2 – 3 – x 4 – 6 x 2 – 3 = 0
⇔ x 4 – 5 x 2 – 6 = 0
Đặt m = x 2 . Điều kiện m ≥ 0
Ta có: x 4 – 5 x 2 – 6 = 0 ⇔ m 2 – 5m – 6 = 0
∆ = - 5 2 – 4.1.(-6) = 25 + 24 = 49 > 0
∆ = 49 = 7
Ta có: x 2 = 6 ⇒ x = ± 6
Vậy phương trình đã cho có 2 nghiệm: x 1 = 6 , x 2 = - 6
PT
1
CM
11 tháng 4 2019
Ta có: x 4 + 2 x 2 – x + 1 = 15 x 2 – x – 35
⇔ x 4 + 2 x 2 – x + 1 - 15 x 2 + x + 35 = 0
⇔ x 4 – 13 x 2 + 36 = 0
Đặt m = x 2 . Điều kiện m ≥ 0
Ta có: x 4 – 13 x 2 + 36 = 0 ⇔ m 2 – 13m + 36 = 0
∆ = - 13 2 – 4.1.36 = 169 – 144 = 25 > 0
∆ = 25 = 5
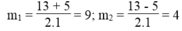
Ta có: x 2 = 9 ⇒ x = ± 3
x 2 = 4 ⇒ x = ± 2
Vậy phương trình đã cho có 4 nghiệm: x 1 = 3; x 2 = -3; x 3 = 2; x 4 = -2
PT
1
CM
24 tháng 4 2017
Ta có: x 3 – 5 x 2 –x +5 = 0 ⇔ x 2 ( x -5) – ( x -5) =0
⇔ (x -5)(x2 -1) =0 ⇔ (x -5)(x -1)(x +1) =0
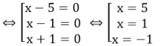
Vậy phương trình đã cho có 3 nghiệm :x1 = 5;x2 =1;x3=-1
4x4 + x2 – 5 = 0;
Đặt x2 = t (t ≥ 0). Phương trình trở thành:
4t2 + t - 5 = 0
Nhận thấy phương trình có dạng a + b + c = 0 nên phương trình có nghiệm
t1 = 1; t2 =(-5)/4
Do t ≥ 0 nên t = 1 thỏa mãn điều kiện
Với t = 1, ta có: x2 = 1 ⇔ x = ±1
Vậy phương trình có 2 nghiệm x1 = 1; x2 = -1