Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow2x^2+3x-2-2\le2x^2+2x-3\Leftrightarrow x+1\le0\Leftrightarrow x\le1\)

a: \(x^3+8x=5x^2+4\)
=>\(x^3-5x^2+8x-4=0\)
=>\(x^3-x^2-4x^2+4x+4x-4=0\)
=>\(x^2\left(x-1\right)-4x\left(x-1\right)+4\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(x^2-4x+4\right)=0\)
=>\(\left(x-1\right)\left(x-2\right)^2=0\)
=>\(\left[{}\begin{matrix}x-1=0\\\left(x-2\right)^2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
2: \(x^3+3x^2=x+6\)
=>\(x^3+3x^2-x-6=0\)
=>\(x^3+2x^2+x^2+2x-3x-6=0\)
=>\(x^2\cdot\left(x+2\right)+x\left(x+2\right)-3\left(x+2\right)=0\)
=>\(\left(x+2\right)\left(x^2+x-3\right)=0\)
=>\(\left[{}\begin{matrix}x+2=0\\x^2+x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{-1+\sqrt{13}}{2}\\x=\dfrac{-1-\sqrt{13}}{2}\end{matrix}\right.\)
3: ĐKXĐ: x>=0
\(2x+3\sqrt{x}=1\)
=>\(2x+3\sqrt{x}-1=0\)
=>\(x+\dfrac{3}{2}\sqrt{x}-\dfrac{1}{2}=0\)
=>\(\left(\sqrt{x}\right)^2+2\cdot\sqrt{x}\cdot\dfrac{3}{4}+\dfrac{9}{16}-\dfrac{17}{16}=0\)
=>\(\left(\sqrt{x}+\dfrac{3}{4}\right)^2=\dfrac{17}{16}\)
=>\(\left[{}\begin{matrix}\sqrt{x}+\dfrac{3}{4}=-\dfrac{\sqrt{17}}{4}\\\sqrt{x}+\dfrac{3}{4}=\dfrac{\sqrt{17}}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=\dfrac{\sqrt{17}-3}{4}\left(nhận\right)\\\sqrt{x}=\dfrac{-\sqrt{17}-3}{4}\left(loại\right)\end{matrix}\right.\)
=>\(x=\dfrac{13-3\sqrt{17}}{8}\left(nhận\right)\)
4: \(x^4+4x^2+1=3x^3+3x\)
=>\(x^4-3x^3+4x^2-3x+1=0\)
=>\(x^4-x^3-2x^3+2x^2+2x^2-2x-x+1=0\)
=>\(x^3\left(x-1\right)-2x^2\left(x-1\right)+2x\left(x-1\right)-\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(x^3-2x^2+2x-1\right)=0\)
=>\(\left(x-1\right)\left(x^3-x^2-x^2+x+x-1\right)=0\)
=>\(\left(x-1\right)^2\cdot\left(x^2-x+1\right)=0\)
=>(x-1)^2=0
=>x-1=0
=>x=1
a.
\(x^3+8x=5x^2+4\)
\(\Leftrightarrow x^3-5x^2+8x-4=0\)
\(\Leftrightarrow\left(x^3-4x^2+4x\right)-\left(x^2-4x+4\right)=0\)
\(\Leftrightarrow x\left(x-2\right)^2-\left(x-2\right)^2=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
b.
\(x^3+3x^2-x-6=0\)
\(\Leftrightarrow\left(x^3+x^2-3x\right)+\left(2x^2+2x-6\right)=0\)
\(\Leftrightarrow x\left(x^2+x-3\right)+2\left(x^2+x-3\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2+x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{-1\pm\sqrt{13}}{2}\end{matrix}\right.\)

a/ Với x = - 1 thì BĐT đúng.
Xét \(x\ne-1\)
Ta có: \(x^3+\left(3x^2-4x-4\right)\sqrt{x+1}\le0\)
\(\Leftrightarrow x^3+3x^2\sqrt{x+1}-4\sqrt{\left(x+1\right)^3}\le0\)
\(\Leftrightarrow\frac{x^3}{\sqrt{\left(x+1\right)^3}}+3.\frac{x^2}{\sqrt{\left(x+1\right)^2}}-4\le0\)
Đặt \(\frac{x}{\sqrt{x+1}}=t\)thì ta có bpt thành
\(t^3+3t^2-4\le0\)
\(\Leftrightarrow\left(t-1\right)\left(t+2\right)^2\le0\)
Tới đây thì đơn giản rồi b làm tiếp nhé.
Câu b còn lại mình nghĩ chỉ cần bình phương rồi chuyển cái chứa căn sang 1 bên không chứa căn sang 1 bên. Sau đó bình phương thêm 1 lần nữa rồi đặt nhân tử chung là ra :)

@Nguyễn Việt Lâm @Uyen Vuuyen @Trần Trung Nguyên
@JakiNatsumi @Vương Đại Nguyên
\(\Leftrightarrow\left|x^2-x+1\right|< =\left|x^2-3x+4\right|\)
\(\Leftrightarrow\left(x^2-x+1\right)^2< =\left(x^2-3x+4\right)^2\)
\(\Leftrightarrow\left(x^2-3x+4\right)^2>=\left(x^2-x+1\right)^2\)
=>(x^2-3x+4-x^2+x-1)(x^2-3x+4+x^2-x+1)>=0
=>(-2x+3)(2x^2-4x+5)>=0
=>-2x+3>=0
=>-2x>=-3
=>x<=3/2

\(\Leftrightarrow\left|x^2-x+1\right|< =\left|x^2-3x+4\right|\)
\(\Leftrightarrow\left|x^2-x+1\right|< =x^2-3x+4\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-x+1< =x^2-3x+4\\x^2-x+1>=-x^2+3x-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2x< =3\\2x^2-4x+5>=0\end{matrix}\right.\Leftrightarrow x>=-\dfrac{3}{2}\)

Vì là trắc nghiệm nên mình làm tắt thôi nkaaa.
Thay `x=1/4` vào từng ý:
a: `0=0 =>` Đúng.
b. `23/4 = 5` => Sai.

a) \(\sqrt{-x^2+x+4}=x-3\left(đk:x\ge3\right)\)
\(-x^2+x+4=x^2-6x+9\)
\(2x^2-7x-5=0\)
\(\Delta=49-4.2.\left(-5\right)=89\)
\(\left[{}\begin{matrix}x=\dfrac{7+\sqrt{89}}{4}\left(TM\right)\\x=\dfrac{7-\sqrt{89}}{4}\left(L\right)\end{matrix}\right.\)
b) \(\sqrt{-2x^2+6}=x-1\left(đk:x\ge1\right)\)
\(-2x^2+6=x^2-2x+1\)
\(3x^2-2x-5=0\)
\(\Delta=4+4.3.5=64\)
\(\left[{}\begin{matrix}x=\dfrac{2-8}{6}=-1\left(L\right)\\x=\dfrac{2+8}{6}=\dfrac{5}{3}\left(TM\right)\end{matrix}\right.\)
c) \(\sqrt{x+2}=1+\sqrt{x-3}\left(Đk:x\ge3\right)\)
\(x+2=1+x-3+2\sqrt{x-3}\)
\(\sqrt{x-3}=2\)
\(x-3=4\)
\(x=7\)

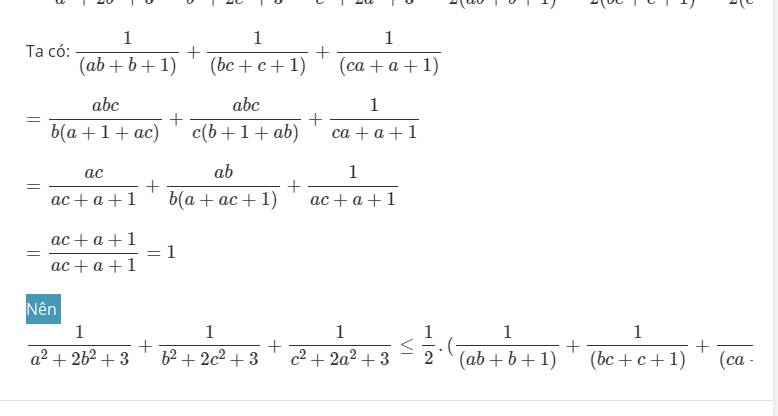


a: \(x^2-3x+1>2\left(x-1\right)-x\left(3-x\right)\)
=>\(x^2-3x+1>2x-2-3x+x^2\)
=>-3x+1>-x-2
=>-2x>-3
=>\(x< \dfrac{3}{2}\)
b: \(\left(x-1\right)^2+x^2< =\left(x+1\right)^2+\left(x+2\right)^2\)
=>\(x^2-2x+1+x^2< =x^2+2x+1+x^2+4x+4\)
=>-2x+1<=6x+5
=>-7x<=4
=>\(x>=-\dfrac{4}{7}\)
c:
\(\left(x^2+1\right)\left(x-6\right)< =\left(x-2\right)^3\)
=>\(x^3-6x^2+x-6< =x^3-6x^2+12x-8\)
=>x-6<=12x-8
=>-11x<=-8+6=-2
=>\(x>=\dfrac{2}{11}\)