K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2022
a.
\(3\sqrt{-x^2+x+6}\ge2\left(1-2x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-x^2+x+6\ge0\\1-2x< 0\end{matrix}\right.\\\left\{{}\begin{matrix}1-2x\ge0\\9\left(-x^2+x+6\right)\ge4\left(1-2x\right)^2\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-2\le x\le3\\x>\dfrac{1}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\25\left(x^2-x-2\right)\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}< x\le3\\\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\-1\le x\le2\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow-1\le x\le3\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2022
b.
ĐKXĐ: \(x\ge0\)
\(\Leftrightarrow\sqrt{2x^2+8x+5}-4\sqrt{x}+\sqrt{2x^2-4x+5}-2\sqrt{x}=0\)
\(\Leftrightarrow\dfrac{2x^2+8x+5-16x}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{2x^2-4x+5-4x}{\sqrt{2x^2-4x+5}+2\sqrt{x}}=0\)
\(\Leftrightarrow\dfrac{2x^2-8x+5}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{2x^2-8x+5}{\sqrt{2x^2-4x+5}+2\sqrt{x}}=0\)
\(\Leftrightarrow\left(2x^2-8x+5\right)\left(\dfrac{1}{\sqrt{2x^2+8x+5}+4\sqrt{x}}+\dfrac{1}{\sqrt{2x^2-4x+5}+2\sqrt{x}}\right)=0\)
\(\Leftrightarrow2x^2-8x+5=0\)
\(\Leftrightarrow x=\dfrac{4\pm\sqrt{6}}{2}\)
17 tháng 2 2022
\(\dfrac{3}{x-2}\ge\dfrac{5}{2x-1}.\\ \Leftrightarrow\dfrac{3}{x-2}-\dfrac{5}{2x-1}\ge0.\\ \Leftrightarrow\dfrac{6x-3-5x+10}{\left(x-2\right)\left(2x-1\right)}\ge0.\\ \Leftrightarrow\dfrac{x+7}{\left(x-2\right)\left(2x-1\right)}\ge0.\)
Ta có:
\(x+7=0.\Leftrightarrow x=-7.\\ x-2=0.\Leftrightarrow x=2.\\ 2x-1=0.\Leftrightarrow x=\dfrac{1}{2}.\)
Đặt \(f\left(x\right)=\dfrac{x+7}{\left(x-2\right)\left(2x-1\right)}.\)
Bảng xét dấu:
\(x\) \(-\infty\) \(-7\) \(\dfrac{1}{2}\) \(2\) \(+\infty\)
\(x+7\) - 0 + | + | +
\(x-2\) - | - | - 0 +
\(2x-1\) - | - 0 + | +
\(f\left(x\right)\) - 0 + || - || +
Vậy \(f\left(x\right)\ge0.\Leftrightarrow x\in[-7;\dfrac{1}{2})\cup\left(2;+\infty\right).\)
6 tháng 4 2020
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
7 tháng 4 2020
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
MS
2
TQ
28 tháng 1 2022
1) \(ĐK:x\ne2\)
Nếu \(x>2\)
BPT ⇔ \(x^2-2x+5-\left(x-1\right)\left(x-2\right)\ge0\) ⇔ \(x^2-2x+5-\left(x^2-3x+3\right)\ge0\)
⇔\(x+2\ge0\) ⇔\(x\ge-2\) ⇒ Lấy \(x\ge2\)
Nếu \(x< 2\)
BPT ⇔\(\dfrac{-\left(x^2-2x+5\right)}{x-2}-x+1\ge0\) ⇔\(-x^2+2x-5-\left(x-1\right)\left(x-2\right)\ge0\)
⇔\(-x^2+2x-5-x^2+3x-2\ge0\)
⇔\(-2x^2+5x-7\ge0\)
⇔\(x^2-\dfrac{5}{2}x+\dfrac{7}{2}\le0\)
⇔\(\left(x-\dfrac{5}{4}\right)^2\le\dfrac{11}{4}\)
⇔\(\left[{}\begin{matrix}x-\dfrac{5}{4}\le\dfrac{11}{4}\\x-\dfrac{5}{4}\le\dfrac{-11}{4}\end{matrix}\right.\) ⇔\(\left[{}\begin{matrix}x\le4\\x\le\dfrac{-3}{2}\end{matrix}\right.\) ⇔ \(x\le\dfrac{-3}{2}\)
S= [2;+∞)U(-∞;\(\dfrac{-3}{2}\)]
TQ
28 tháng 1 2022
2) \(ĐK:x\ne-1\)
Nếu \(x>-1\)
BPT ⇔ \(2x-3-2\left(x+1\right)< 0\) ⇔\(2x-3-2x-2< 0\)
⇔\(-5< 0\) ( luôn đúng với mọi \(x>-1\))
Nếu \(x< -1\)
BPT⇔\(\dfrac{-\left(2x-3\right)}{x+1}-2< 0\) ⇔\(-\left(2x-3\right)-2\left(x+1\right)< 0\) ⇔\(-4x+1< 0\) ⇔ \(x>\dfrac{-1}{4}\)
Vậy S=....
AH
Akai Haruma
Giáo viên
15 tháng 3 2021
Lời giải:
b/
\(\frac{3x+5}{2x^2-5x+3}\geq 0\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} 3x+5\geq 0\\ 2x^2-5x+3>0\end{matrix}\right.\\ \left\{\begin{matrix} 3x+5\leq 0\\ 2x^2-5x+3<0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} x\geq \frac{-5}{3}\\ x>\frac{3}{2}(\text{hoặc}) x< 1\end{matrix}\right.\\ \left\{\begin{matrix} x\leq \frac{-5}{3}\\ 1< x< \frac{3}{2}\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow \left[\begin{matrix} x>\frac{3}{2}\\ \frac{-5}{3}\leq x< 1\end{matrix}\right.\ \)
c/
$2x^3+x+3>0$
$\Leftrightarrow 2x^2(x+1)-2x(x+1)+3(x+1)>0$
$\Leftrightarrow (x+1)(2x^2-2x+3)>0$
$\Leftrightarrow (x+1)[x^2+(x-1)^2+2]>0$
$\Leftrightarrow x+1>0$
$\Leftrightarrow x>-1$
28 tháng 1 2022
1: \(\Leftrightarrow\left[{}\begin{matrix}2x-3>5\\2x-3< -5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>5\\x< -1\end{matrix}\right.\)
2: \(\Leftrightarrow-4< =2x-1< =4\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-1>=-4\\2x-1< =4\end{matrix}\right.\Leftrightarrow\dfrac{-3}{2}< =x< =\dfrac{5}{2}\)
HP
16 tháng 3 2021
1.
ĐK: \(x\ne7;x\ne-1;x\ne3\)
\(\dfrac{2x-5}{x^2-6x-7}\le\dfrac{1}{x-3}\left(1\right)\)
TH1: \(x< -1\)
\(\left(1\right)\Leftrightarrow\left(2x-5\right)\left(x-3\right)\ge x^2-6x-7\)
\(\Leftrightarrow2x^2-11x+15\ge x^2-6x-7\)
\(\Leftrightarrow x^2-5x+22\ge0\)
\(\Leftrightarrow\) Bất phương trình đúng với mọi \(x< -1\)
TH2: \(-1< x< 3\)
\(\left(1\right)\Leftrightarrow\left(3-x\right)\left(2x-5\right)\ge\left(7-x\right)\left(x+1\right)\)
\(\Leftrightarrow-2x^2+11x-15\ge-x^2+6x+7\)
\(\Leftrightarrow-x^2+5x-22\ge0\)
\(\Rightarrow\) vô nghiệm
TH3: \(3< x< 7\)
Khi đó \(\dfrac{2x-5}{x^2-6x-7}\le0\); \(\dfrac{1}{x-3}>0\)
\(\Rightarrow\) Bất phương trình đúng với mọi \(3< x< 7\)
TH4: \(x>7\)
\(\left(1\right)\Leftrightarrow\left(2x-5\right)\left(x-3\right)\le x^2-6x-7\)
\(\Leftrightarrow2x^2-11x+15\le x^2-6x-7\)
\(\Leftrightarrow x^2-5x+22\le0\)
\(\Rightarrow\) vô nghiệm
Vậy ...
Các bài kia tương tự, chứ giải ra mệt lắm.
15 tháng 7 2023
1) \(\sqrt[]{3x+7}-5< 0\)
\(\Leftrightarrow\sqrt[]{3x+7}< 5\)
\(\Leftrightarrow3x+7\ge0\cap3x+7< 25\)
\(\Leftrightarrow x\ge-\dfrac{7}{3}\cap x< 6\)
\(\Leftrightarrow-\dfrac{7}{3}\le x< 6\)
28 tháng 1 2022
4: =>2x-3>5 hoặc 2x-3<-5
=>x>4 hoặc x<-1
5: =>-4<=2x-1<=4
=>-3/2<=x<=5/2
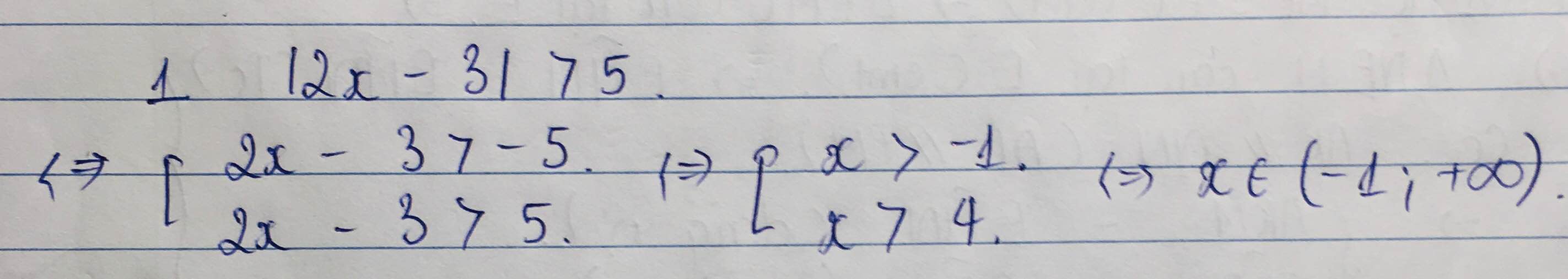
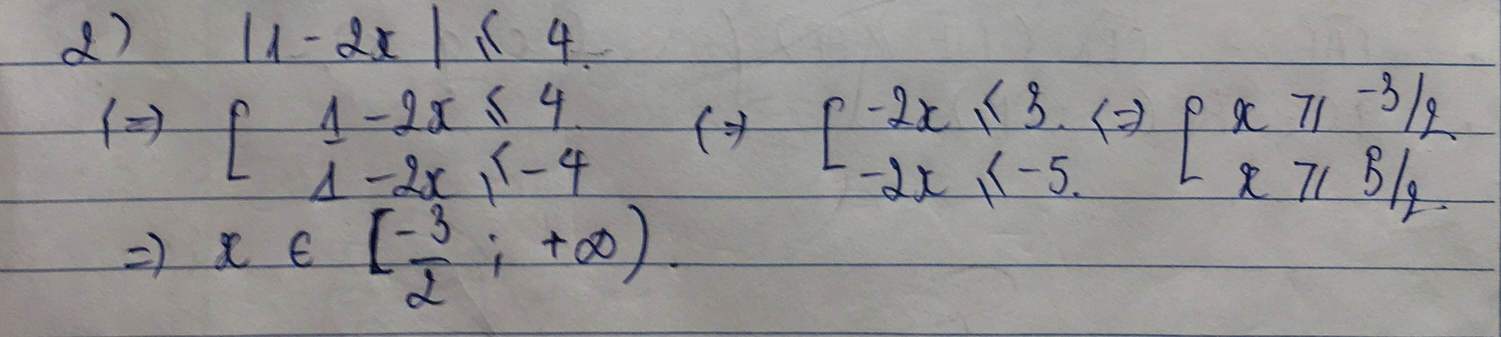
\(\dfrac{3}{x-2}\ge\dfrac{5}{2x-1}\)
ĐKXĐ: x ≠ 2; \(x\ne\dfrac{1}{2}\)
\(\dfrac{3}{x-2}\ge\dfrac{5}{2x-1}\)
\(\Leftrightarrow\dfrac{3}{x-2}-\dfrac{5}{2x-1}\ge0\)
\(\Leftrightarrow\dfrac{3\left(2x-1\right)-5\left(x-2\right)}{\left(x-2\right)\left(2x-1\right)}\ge0\)
\(\Leftrightarrow\dfrac{x+7}{\left(x-2\right)\left(2x-1\right)}\ge0\)
*Với: \(\dfrac{x+7}{\left(x-2\right)\left(2x-1\right)}=0\)
=> x + 7 = 0
<=> x =-7
*Với \(\dfrac{x+7}{\left(x-2\right)\left(2x-1\right)}>0\) (1)
Ta lâpj bảng xét dấu:
x
-7
1/2
2
X + 7
-
0
+
|
+
|
+
2x – 1
-
|
-
0
+
|
+
X - 2
-
|
-
|
-
0
+
BĐT (1)
-
0
+
||
-
||
+
Từ bảng trên ta có thể thấy: \(\dfrac{x+7}{\left(x-2\right)\left(2x-1\right)}>0\) khi -7 < x < 1/2 hoăcj x > 2
Vayj:.............