K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 10 2021
a: Gọi (d): y=ax+b là đường thẳng cần tìm
Theo đề, ta có:
\(\left\{{}\begin{matrix}0a+b=0\\-2a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=0\\a=-2\end{matrix}\right.\)
19 tháng 2 2023
x và y tỉ lệ thuận
nên \(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}\)
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{2x_1-3x_2}{2y_1-3y_2}=\dfrac{42.5}{-8.5}=-5\)
=>x=-5y
14 tháng 8 2023
4:
a: =>2/5x+7/20-2/20=1/10
=>2/5x+5/20=1/10
=>2/5x=1/10-1/4=4/40-10/40=-6/40=-3/20
=>x=-3/20:2/5=-3/20*5/2=-15/40=-3/8
b: 3/2-1/2x=-1/3+3=8/3
=>1/2x=3/2-8/3=9/6-16/6=-7/6
=>x=-7/6*2=-7/3
c: 15/8-1/8:(1/4x-0,5)=5/4
=>1/8:(1/4x-1/2)=15/8-5/4=15/8-10/8=5/8
=>1/4x-1/2=1/8:5/8=1/5
=>1/4x=1/5+1/2=7/10
=>x=7/10*4=28/10=2,8
d: \(\Leftrightarrow\left[\left(x+\dfrac{1}{2}\right)^3-\dfrac{5}{4}\right]=\dfrac{11}{4}-\dfrac{5}{8}=\dfrac{22-5}{8}=\dfrac{17}{8}\)
=>\(\left(x+\dfrac{1}{2}\right)^3=\dfrac{17}{8}+\dfrac{5}{4}=\dfrac{27}{8}\)
=>x+1/2=3/2
=>x=1
25 tháng 7 2021
a) Để f(x) có bậc là 1 thì m=0
b) Thay x=-1 vào f(x), ta được:
\(m\cdot\left(-1\right)^2+3\cdot\left(-1\right)+6=0\)
\(\Leftrightarrow m+3=0\)
hay m=-3
13 tháng 1 2022
a: Xét ΔADI và ΔAEI có
AD=AE
\(\widehat{DAI}=\widehat{EAI}\)
AI chung
DO đó: ΔADI=ΔAEI
Suy ra: DI=EI
hay I là trung điểm của DE
b: Xét ΔNID vuông tại I và ΔNIE vuông tại I có
NI chung
ID=IE
Do đó: ΔNID=ΔNIE
Suy ra: ND=NE
TN
1
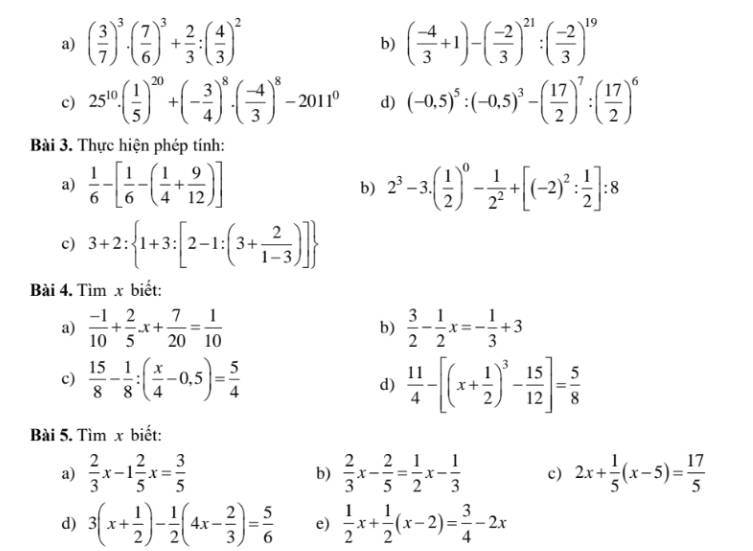
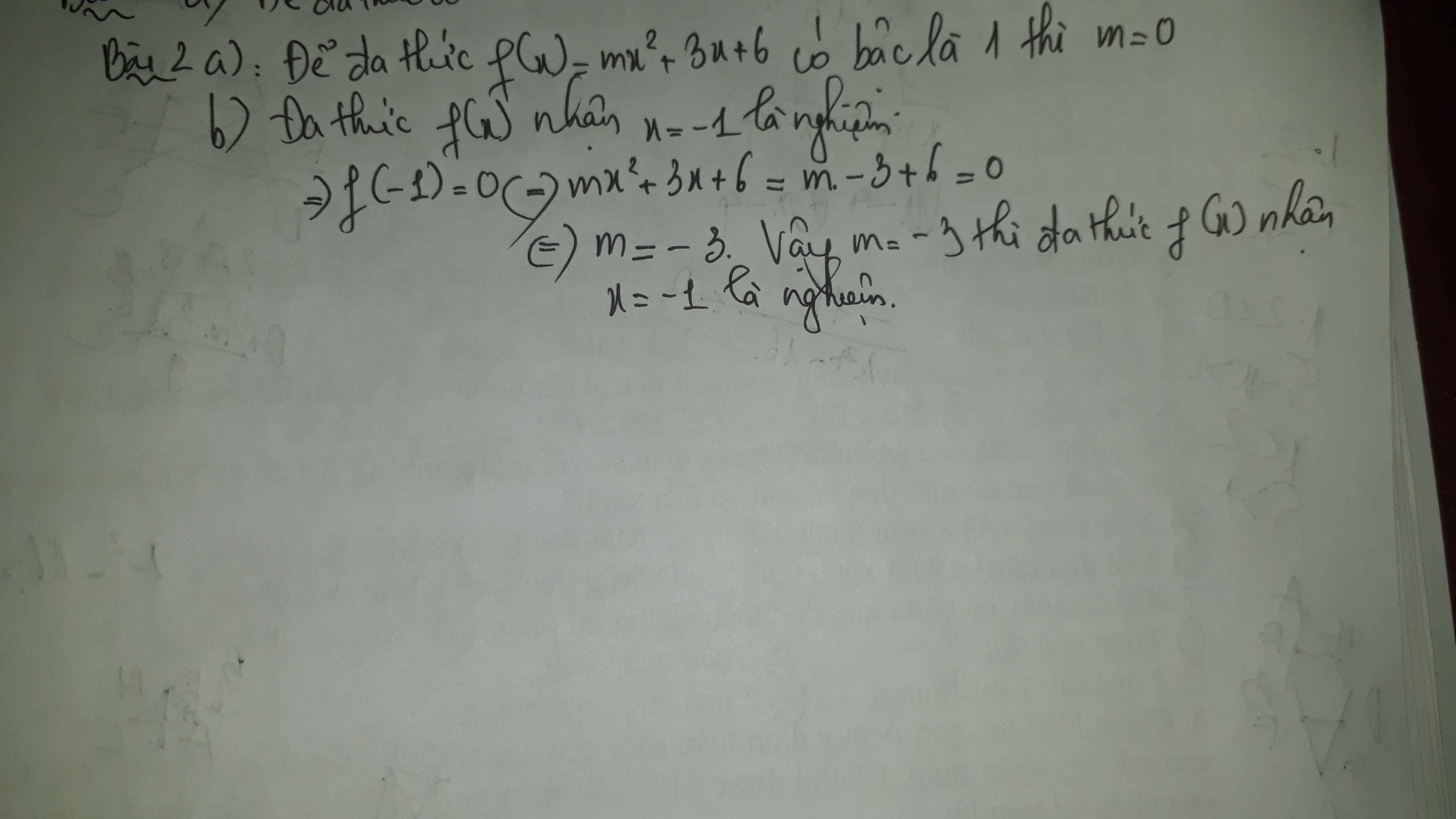
Ta có: \(x^2+y^2+z^2+\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}=6 \)
\(\Leftrightarrow x^2+y^2+z^2+\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}-6=0\\ \Leftrightarrow\left(x^2+\dfrac{1}{x^2}-2\right)+\left(y^2+\dfrac{1}{y^2}-2\right)+\left(z^2+\dfrac{1}{z^2}-2\right)=0\\ \Leftrightarrow\left(x^2-2\cdot x^2\cdot\dfrac{1}{x^2}+\dfrac{1}{x^2}\right)+\left(y^2-2\cdot y^2\cdot\dfrac{1}{y^2}+\dfrac{1}{y^2}\right)+\left(z^2-2\cdot z^2\cdot\dfrac{1}{z^2}+\dfrac{1}{z^2}\right)=0\\ \Leftrightarrow\left(x-\dfrac{1}{x}\right)^2+\left(y-\dfrac{1}{y}\right)^2+\left(z-\dfrac{1}{z}\right)^2=0\)
Mà: \(\left\{{}\begin{matrix}\left(x-\dfrac{1}{x}\right)^2\ge0\forall x\\\left(y-\dfrac{1}{y}\right)^2\ge0\forall y\\\left(z-\dfrac{1}{z}\right)^2\ge0\forall z\end{matrix}\right.=>\left(x-\dfrac{1}{x}\right)^2+\left(y-\dfrac{1}{y}\right)^2+\left(z-\dfrac{1}{z}\right)^2\ge0\forall x,y,z\)
Dấu "=" xảy ra khi: \(\left\{{}\begin{matrix}x=\dfrac{1}{x}\\y=\dfrac{1}{y}\\z=\dfrac{1}{z}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2=1\\y^2=1\\z^2=1\end{matrix}\right.\)
\(P=x^{2024}+y^{2024}+z^{2024}\\=\left(x^2\right)^{1012}+\left(y^2\right)^{1012}+\left(z^2\right)^{1012}\\ =1^{1012}+1^{1012}+1^{1012}=3\)