K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 1 2022
b: Gọi A là Tọa độ giao điểm của hàm số với trục tung
=>Tọa độ của A là:
\(\left\{{}\begin{matrix}x=0\\y=\left(m-2\right)\cdot0+m+3=m+3\end{matrix}\right.\)
Gọi B là Tọa độ giao điểm của hàm số với trục hoành
=>Tọa độ của B là:
\(\left\{{}\begin{matrix}\left(m-2\right)\cdot x+m+3=0\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-m-3}{m-2}\\y=0\end{matrix}\right.\)
Theo đề, ta có: \(\left|m+3\right|=\left|\dfrac{-m-3}{m-2}\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}m+3=\dfrac{-m-3}{m-2}\\m+3=\dfrac{m+3}{m-2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m^2+m-6+m+3=0\\m^2+m-6-m-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(m+3\right)\left(m-1\right)=0\\\left(m+3\right)\left(m-3\right)=0\end{matrix}\right.\Leftrightarrow m\in\left\{-3;1;3\right\}\)
5 tháng 11 2021
a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=-20\\3a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=7\\b=8-3a=8-3\cdot7=-13\end{matrix}\right.\)
HB
2
12 tháng 10 2021
\(\left(3\sqrt{7}\right)^2=63>28=\left(\sqrt{28}\right)^2\) hoặc \(3\sqrt{7}>2\sqrt{7}=\sqrt{28}\)
AH
Akai Haruma
Giáo viên
29 tháng 6 2021
1.
$(m^2-m-1)x-5m=(3-m)x$
$\Leftrightarrow (m^2-m-1+m-3)x=5m$
$\Leftrightarrow (m^2-4)x=5m$
$\Leftrightarrow (m-2)(m+2)x=5m$
Nếu $m=-2$ thì $0x=-10$ (vô lý) $\Rightarrow$ pt vô nghiệm
Nếu $m=2$ thì $0x=10$ (vô lý) $\Rightarrow$ pt vô nghiệm
Nếu $m\neq \pm 2$ thì pt có nghiệm duy nhất $x=\frac{5m}{(m-2)(m+2)}$
AH
Akai Haruma
Giáo viên
29 tháng 6 2021
2.
$m^2x+mx+x-m-2=0$
$\Leftrightarrow x(m^2+m+1)=m+2$
Vì $m^2+m+1=(m+\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}>0$ với mọi $m\in\mathbb{R}$
$\Rightarrow m^2+m+1\neq 0$
Do đó pt có nghiệm duy nhất $x=\frac{m+2}{m^2+m+1}$ với mọi $m\in\mathbb{R}$
YN
2
22 tháng 9 2021
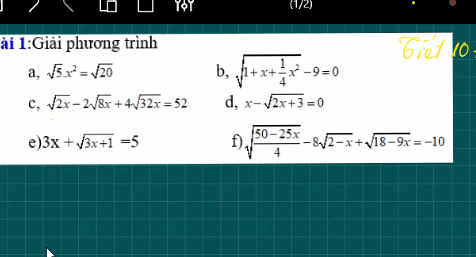
a) \(\Leftrightarrow x^2=\sqrt{4}\)
\(\Leftrightarrow x^2=2\Leftrightarrow x=\pm2\)
b) \(\Leftrightarrow\sqrt{\left(\dfrac{1}{2}x+1\right)^2}=9\)
\(\Leftrightarrow\left|\dfrac{1}{2}x+1\right|=9\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x+1=9\\\dfrac{1}{2}x+1=-9\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=16\\x=-16\end{matrix}\right.\)
c) \(\Leftrightarrow\sqrt{2x}-4\sqrt{2x}+16\sqrt{2x}=52\left(đk:x\ge0\right)\)
\(\Leftrightarrow13\sqrt{2x}=52\Leftrightarrow\sqrt{2x}=4\Leftrightarrow2x=16\Leftrightarrow x=8\left(tm\right)\)
22 tháng 9 2021
f: Ta có: \(\sqrt{\dfrac{50-25x}{4}}-8\sqrt{2-x}+\sqrt{18-9x}=-10\)
\(\Leftrightarrow\sqrt{2-x}\cdot\dfrac{5}{2}-8\sqrt{2-x}+3\sqrt{2-x}=-10\)
\(\Leftrightarrow\sqrt{2-x}=4\)
\(\Leftrightarrow2-x=16\)
hay x=-14
NT
1
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 7 2021
2.1
ĐKXĐ: \(x\ge-\dfrac{1}{16}\)
\(x^2-x-20-2\left(\sqrt{16x+1}-9\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4\right)-\dfrac{32\left(x-5\right)}{\sqrt{16x+1}+9}=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4-\dfrac{32}{\sqrt{16x+1}+9}\right)=0\) (1)
Do \(x\ge-\dfrac{1}{16}\Rightarrow\left\{{}\begin{matrix}\dfrac{32}{\sqrt{16x+1}+9}< \dfrac{32}{9}\\x+4\ge-\dfrac{1}{16}+4=\dfrac{63}{16}>\dfrac{32}{9}\end{matrix}\right.\)
\(\Rightarrow x+4-\dfrac{32}{\sqrt{16x+1}+9}>0\)
Nên (1) tương đương:
\(x-5=0\)
\(\Leftrightarrow x=5\)
Câu 2.2, 2.3 đề lỗi không dịch được
6 tháng 12 2021
a: Xét ΔSAB và ΔSCA có
\(\widehat{S}\) chung
\(\widehat{SAB}=\widehat{SCA}\)
Do đó: ΔSAB\(\sim\)ΔSCA
Số tiền mua bút bi và bút chì là \(279000-45000\cdot3=144000\left(đồng\right)\)
Tổng số bút bi và bút chì màu là 36 chiếc nên x+y=36
Số tiền mua bút bi là 3600x(đồng)
Số tiền mua bút chì màu là 5000y(đồng)
Tổng số tiền là 144000 đồng nên 3600x+5000y=144000
=>36x+50y=144
=>18x+25y=72
Do đó, hệ hai phương trình là: \(\left\{{}\begin{matrix}x+y=36\\18x+25y=72\end{matrix}\right.\)