
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow\left|5-2x\right|=\dfrac{7,5+4,5}{4}=3\\ \Leftrightarrow\left[{}\begin{matrix}5-2x=3\\2x-5=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)

Câu 1 mình nghĩ nó khá đơn giản rồi, bạn tính ra ngay thôi
Câu 2: Mình nghĩ là tìm min chứ ko phải max
Vì \(\left(-\frac{2}{3}+\frac{1}{2}x\right)^2\ge0\Rightarrow A=\left(-\frac{2}{3}+\frac{1}{2}x\right)^2-2,5\ge2,5\)
\(\Rightarrow A_{min}=2,5\Leftrightarrow\left(-\frac{2}{3}+\frac{1}{2}x\right)^2=0\Leftrightarrow-\frac{2}{3}+\frac{1}{2}x=0\Leftrightarrow\frac{1}{2}x=\frac{2}{3}\Leftrightarrow x=\frac{4}{3}\)
A đạt giá trị nhỏ nhất là 2,5 khi x=4/3
Câu 3:
\(x=\frac{26}{7+b}\) âm khi 7+b âm <=> 7+b<0 <=> b<-7
vì b là số nguyên lớn nhất nên b=-8

\(\frac{x}{-10}=\frac{3,6}{2,5}\)
\(\Rightarrow\frac{x}{-10}=1,44\)
\(\Rightarrow x=1,44\text{}\text{}\times\left(-10\right)\)
\(\Rightarrow x=-14,4\)
Vậy x = -14,4
_Chúc bạn học tốt_

\(\frac{a}{b}=\frac{-2,5}{4,5}\Rightarrow\frac{a}{-2,5}=\frac{b}{4,5}\)
áp dụng ...ta có
\(\frac{a}{-2,5}=\frac{b}{4,5}=\frac{a+b}{-2,5+4,5}=\frac{1,44}{2}=0,72\)
\(\frac{a}{-2,5}=0,72\Rightarrow a=0,72.\left(-2,5\right)=-1,8\)
\(\frac{b}{4,5}=0,72\Rightarrow b=0,72.4,5=3.24\)

a/b=-2,5/4,5=-5/9
=> a gồm -5 phần bằng nhau thì b gồm 9 phần bằng nhau
=> a+b gồm -5 + 9=4 phần bằng nhau => 1,44 gồm 4 phần bằng nhau
=> 1 phần bằng 1,44 : 4 = 0,36
=> a=0,36 x (-5)=-1,8
b=0,36 x 9 =-3,24

Câu 1:
Ta thấy:
\(\left(x-\frac{2}{5}\right)^2\ge0\Rightarrow\frac{1}{3}\cdot\left(x-\frac{2}{5}\right)^2\ge0\)
\(\left|2y+1\right|\ge0\)
\(\Rightarrow\frac{1}{3}\cdot\left(x-\frac{2}{5}\right)^2+\left|2y+1\right|\ge0\)
\(\Rightarrow\frac{1}{3}\cdot\left(x-\frac{2}{5}\right)^2+\left|2y+1\right|-2,5\ge-2,5\)
hay \(A\ge-2,5\)
Dấu "=" xảy ra khi \(\begin{cases}\left(x-\frac{2}{5}\right)^2=0\\\left|2y+1\right|=0\end{cases}\)
\(\Rightarrow\begin{cases}x-\frac{2}{5}=0\\2y+1=0\end{cases}\)
\(\Rightarrow\begin{cases}x=\frac{2}{5}\\2y=-1\end{cases}\)
\(\Rightarrow\begin{cases}x=\frac{2}{5}\\y=-\frac{1}{2}\end{cases}\)
Vậy GTNN của A là -2,5 đạt được khi \(\begin{cases}x=\frac{2}{5}\\y=-\frac{1}{2}\end{cases}\)

\(\frac{x}{2^2}+\frac{x}{2^3}+\frac{x}{2^4}=\frac{x}{3^2}+\frac{x}{3^3}+\frac{x}{3^4}\)
\(\Rightarrow\frac{x}{2^2}+\frac{x}{2^3}+\frac{x}{2^4}-\frac{x}{3^2}-\frac{x}{3^3}-\frac{x}{3^4}=0\)
\(x\left(\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}-\frac{1}{3^2}-\frac{1}{3^3}-\frac{1}{3^4}\right)=0\)
Mà \(\left(\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}-\frac{1}{3^2}-\frac{1}{3^3}-\frac{1}{3^4}\right)\ne0\)
\(\Rightarrow x=0\)
\(\frac{x}{2^2}+\frac{x}{2^3}+\frac{x}{2^4}=\frac{x}{3^2}+\frac{x}{3^3}+\frac{x}{3^4}\)
\(\Leftrightarrow\frac{x}{2^2}+\frac{x}{2^3}+\frac{x}{2^4}-\frac{x}{3^2}-\frac{x}{3^3}-\frac{x}{3^4}=0\)
\(\Leftrightarrow x\left(\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}-\frac{1}{3^2}-\frac{1}{3^3}-\frac{1}{3^4}\right)=0\)
\(\Leftrightarrow x=0\). Do \(\Leftrightarrow x=0\)
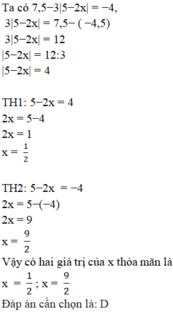
x+3,25=4,5
x=4,5-3,25
x=1,25