Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TXĐ: \(D=R\)
\(f'\left(x\right)=4x^3-24x\)
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\sqrt{6}\\x=-\sqrt{6}\left(loai\right)\end{matrix}\right.\)
\(\begin{matrix}f\left(0\right)=-1\\f\left(\sqrt{6}\right)=-37\\f\left(9\right)=5588\end{matrix}\)
suy ra chọn D
Chọn C
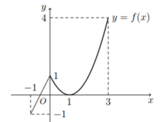
Quan sát đồ thị ta thấy hàm số y = f(x) đạt giá trị nhỏ nhất trên [-1;3] là -1 tại điểm x = =-1 và đạt giá trị lớn nhất trên[-1;3] là 4 tại điểm x = 3. Do đó M = 4, m = -1.
Giá trị M - m = 4 - (-1) = 5.
\(\sqrt{4-x}\ge0\) với mọi x thuộc TXĐ nên \(y=\sqrt{4-x}+\sqrt{3}\ge\sqrt{3}\)
Đáp án D
Chọn D
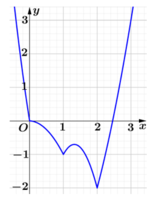
Dựa vào hình vẽ ta có : M = 3, m = -2. Do đó: M + m = 1
Chọn A
Hàm số f(x) = (x-6) x 2 + 4 xác định và liên tục trên đoạn [0;3].
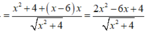
Suy ra 
với a là số nguyên và b, c là các số nguyên dương nên
a = - 12, b = 3, c = 13. Do đó: S = a + b + c = 4.
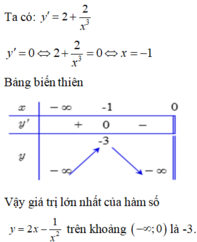
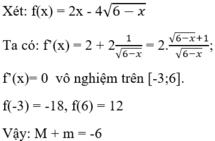
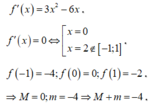
\(y=x+\dfrac{1}{x}-5\ge2\sqrt{x.\dfrac{1}{x}}-5=-3\)
Đáp án C