Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Do \(f\left(x\right)=ax^4+bx^3+cx^2+dx+e\) có 4 nghiệm pb \(x_1;x_2;x_3;x_4\)
\(\Rightarrow f\left(x\right)=a\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)\left(x-x_4\right)\)
Ta có:
\(f'\left(x\right)=a\left[\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)+\left(x-x_2\right)\left(x-x_3\right)\left(x-x_4\right)+\left(x-x_1\right)\left(x-x_3\right)\left(x-x_4\right)+\left(x-x_1\right)\left(x-x_2\right)\left(x-x_4\right)\right]\)
\(\Rightarrow\left\{{}\begin{matrix}f'\left(x_1\right)=a\left(x_1-x_2\right)\left(x_1-x_3\right)\left(x_1-x_4\right)\\f'\left(x_2\right)=a\left(x_2-x_1\right)\left(x_2-x_3\right)\left(x_2-x_4\right)\\f'\left(x_3\right)=a\left(x_3-x_1\right)\left(x_3-x_2\right)\left(x_3-x_4\right)\\f'\left(x_4\right)=a\left(x_4-x_1\right)\left(x_4-x_2\right)\left(x_4-x_3\right)\end{matrix}\right.\)
Mà tiếp tuyến tại A và B vuông góc \(\Leftrightarrow f'\left(x_1\right).f'\left(x_2\right)=-1\) (1)
Do \(x_1;x_2;x_3;x_4\) lập thành 1 CSC, giả sử công sai của CSC là \(d\)
\(\Rightarrow\left\{{}\begin{matrix}x_2=x_1+d\\x_3=x_1+2d\\x_4=x_1+3d\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}f'\left(x_1\right)=a.\left(-d\right).\left(-2d\right).\left(-3d\right)=-6ad^3\\f'\left(x_2\right)=a.d.\left(-d\right).\left(-2d\right)=2ad^3\\f'\left(x_3\right)=a.2d.d.\left(-d\right)=-2ad^3\\f'\left(x_4\right)=a.3d.2d.d=6ad^3\end{matrix}\right.\)
Thế vào (1): \(-12a^2d^6=-1\Leftrightarrow12a^2d^6=1\)
\(\Rightarrow f'\left(x_3\right)+f'\left(x_4\right)=4ad^3\)
\(\Rightarrow S=\left(4ad^3\right)^{2020}=\left(16a^2d^6\right)^{1010}=\left(\dfrac{4}{3}.12a^2d^6\right)^{1010}=\left(\dfrac{4}{3}\right)^{1010}\)
Bài gì mà dễ sợ :(
Chọn B
Vì ba nghiêm phân biệt x 1 , x 2 , x 3 lập thành một cấp số cộng nên ta đặt : x 1 = x 0 + d , x 2 = x 0 , x 3 = x 0 + d ( d ≠ 0 )
Theo giả thuyết Ta có: x3+3x2 – (24+m)x – 26- n= (x – x1)(x-x2)(x-x3)
=(x-xo+d)(x-xo)(x-xo-d)= x3 – 3xox2+ (3xo2-d2)x-xo3+ xod2 với mọi x
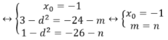
Vậy với m=n thì ba nghiệm phân biệt của phương trình lập thành một cấp số cộng
Chọn C.
Đặt t = x2.
Khi đó ta có phương trình: t2 – 2(m + 1)t + 2m + 1 = 0
Phương trình đã cho có nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt
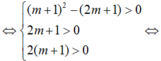
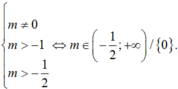
+ Với điều kiện trên thì phương trình (*) có hai nghiệm dương phân biệt là t1; t2.
Khi đó phương trình đã cho có bốn nghiệm phân biệt là 
.
Bốn nghiệm này lập thành một cấp số cộng khi
Theo định lý Vi-ét ta có: t1 + t2 = 2(m + 1) ; t1.t2 = 2m + 1.
Suy ra ta có hệ phương trình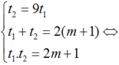 
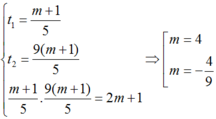
Chỉ có m = 4 thỏa mãn điều kiện .
Do đó 43 = 64.
Giả sử 4 nghiệm phân biệt của phương trình là x1,x2,x3,x4.đặtx2=y≥0, ta được phương trình y2-(3m+5)y+(m+1)2=0(1)
Ta phải tìm m sao cho (1) có hai nghiệm dương phân biệt 0 < y1 < y2. Khi đó thì (1) có bốn nghiệm là: x1=-√(y2),x2=-√(y1,) x3=√(y1),x4=√(y2).
Theo đầu bài bốn nghiệm lập thành một cấp số cộng, nên x3+x1=2x2 và x4+x2=2x3
Áp dụng định lý Vi-et cho phương trình (1). Ta có hệ:
Δ = 3 m + 5 2 − 4 m + 1 2 > 0 S = 3 m + 5 > 0 P = m + 1 2 > 0 ⇔ 5 m 2 + 22 m + 21 > 0 m > − 5 3 m ≠ − 1 ⇔ m > − 7 5 m < − 3 m > − 5 3 m ≠ − 1
⇒ m > − 7 5 và m ≠ − 1
Thay 9 y 1 = y 2 vào định lí Viet y 1 + y 2 = 3 m + 5 y 1 . y 2 = m + 1 2
Giải (*)
19 m 2 − 70 m − 125 = 0 ⇔ m = 5 m = − 25 19
Chọn B
Chọn B.
Đặt t = x2, t ≥ 0.
Phương trình trở thành: t2 – 2(m + 1)t + 2m + 1 = 0 (2)
Phương trình (1) có bốn nghiệm phân biệt khi và chỉ khi PT (2) có hai nghiệm dương phân biệt t2 > t1 > 0.
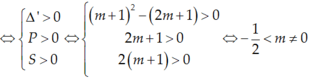
Khi đó PT(2) có bốn nghiệm là: 
Bốn nghiệm này lập thành cấp số cộng khi :
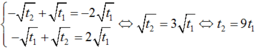
Theo định lý viet thì :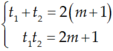 
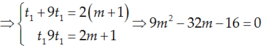
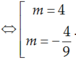
Vậy m = 4 hoặc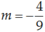 
là những giá trị cần tìm.
Xét hàm số f ( x ) = m x − 1 3 . ( x 2 − 4 ) + x 4 – 3 trên các đoạn [−2; 1], [1; 2]