Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C.
Đặt t = x2.
Khi đó ta có phương trình: t2 – 10t + 2m2 + 7m = 0.
Phương trình đã cho có nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt
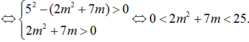
+ Với điều kiện trên thì phương trình(*) có hai nghiệm dương phân biệt là t1, t2(t1 < t2).
Khi đó phương trình đã cho có bốn nghiệm phân biệt là 
Bốn nghiệm này lập thành một cấp số cộng khi
Theo định lý Vi-ét ta có: t1 + t2 = 10 ; t1.t2 = 2m2 + 7m.
Suy ra ta có hệ phương trình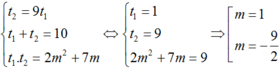 
Cả hai giá trị này đều thỏa mãn điều kiện nên đều có thể nhận được.
Do đó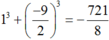 
.
Chọn A.
+ Điều kiện cần: Giả sử phương trình đã cho có ba nghiệm phân biệt x1; x2; x3 lập thành một cấp số nhân.
Theo định lý Vi-ét, ta có x1.x2.x3 = 64
Theo tính chất của cấp số nhân, ta có x1x3 = x22. Suy ra ta có x23 = 64 ⇔ x2 = 4
Thay x = 4 vào phương trình đã cho ta được: 43 – 7m.42 + 2(m2 + 6m).4 – 64 = 0
⇔ m2 – 8m = 0
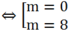
+ Điều kiện đủ: Với m = 0 thay vào phương trình đã cho ta được: x3 – 64 = 0 hay x = 4
(nghiệm kép-loại)
Với m = 8 thay vào phương trình đã cho nên ta có phương trình x3 – 56x2 + 224x – 64 = 0
Giải phương trình này, ta được 3 nghiệm phân biệt lập thành cấp số nhân.
Vậy m = 8 là giá trị cần tìm.
Theo hệ thức Viet: \(x_1+x_2+x_3=-\dfrac{b}{a}=3\)
Do 3 nghiệm lập thành cấp số cộng
\(\Rightarrow x_1+x_2+x_3=3x_2\)
\(\Rightarrow3x_2=3\Rightarrow x_2=1\)
Thế vào pt ban đầu:
\(\Rightarrow1-3+m+2m-1=0\Rightarrow m=1\)
Chọn B.
Đặt t = x2, t ≥ 0.
Phương trình trở thành: t2 – 2(m + 1)t + 2m + 1 = 0 (2)
Phương trình (1) có bốn nghiệm phân biệt khi và chỉ khi PT (2) có hai nghiệm dương phân biệt t2 > t1 > 0.
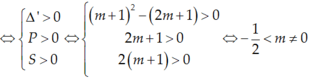
Khi đó PT(2) có bốn nghiệm là: 
Bốn nghiệm này lập thành cấp số cộng khi :
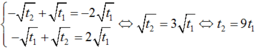
Theo định lý viet thì :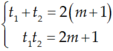 
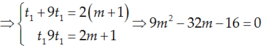
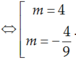
Vậy m = 4 hoặc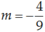 
là những giá trị cần tìm.
Đặt t = x2.
Khi đó ta có phương trình: t2 – 10t + 2m2 + 7m = 0.
Phương trình đã cho có nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt
+ Với điều kiện trên thì phương trình (*) có hai nghiệm dương phân biệt là t1, t2(t1 < t2).
Khi đó phương trình đã cho có bốn nghiệm phân biệt là :
Bốn nghiệm này lập thành một cấp số cộng khi
Theo định lý Vi-ét ta có: t1 + t2 = 10 ; t1.t2 = 2m2 + 7m.
⇒ Ta có hệ phương trình:
Cả hai giá trị này đều thỏa mãn điều kiện nên đều có thể nhận được.
Do đó:
Chọn D.
Cách 1: Giải bài toán như cách giải tự luận.
- Điều kiện cần: Giả sử phương trình đã cho có ba nghiệm phân biệt x1; x2; x3 lập thành một cấp số cộng.
Theo định lý Vi-ét đối với phương trình bậc ba, ta có x1 + x2 + x3 = 3 (1)
Vì x1; x2; x3 lập thành cấp số cộng nên x1 + x3 = 2x2 (2)
Từ (1) và (2) suy ra 3x2 = 3 ⇔ x2 = 1.
Thay x2 = 1 vào phương trình đã cho, ta được
1 - 3.1 - 9.1 + m = 0 suy ra m = 11
- Điều kiện đủ:
+ Với m = 11 thì ta có phương trình x3 – 3x2 – 9x + 11 = 0 ⇔ 
Ba nghiệm này lập thành một cấp số cộng nên m = 11 là giá trị cần tìm.
Chọn B
Đặt t = x 2 , t ≥ 0 .
Phương trình trở thành: t 2 − 2 m + 1 t + 2 m + 1 = 0 (2)
Phương trình (1) có bốn nghiệm phân biệt khi và chỉ khi PT (2) có hai nghiệm dương phân biệt t2 > t1 > 0 .
Δ ' > 0 P > 0 S > 0
⇔ m + 1 2 − 2 m + 1 > 0 2 m + 1 > 0 2 m + 1 > 0 ⇔ − 1 2 < m ≠ 0
Khi đó PT (2) có bốn nghiệm là: − t 2 ; − t 1 ; t 1 ; t 2
Bốn nghiệm này lập thành cấp số cộng khi :
− t 2 + t 1 = − 2 t 1 − t 1 + t 2 = 2 t 1 ⇔ t 2 = 3 t 1 ⇔ t 2 = 9 t 1
Theo định lý viet thì : t 1 + t 2 = 2 m + 1 t 1 t 2 = 2 m + 1
⇒ t 1 + 9 t 1 = 2 m + 1 t 1 9 t 1 = 2 m + 1 ⇔ 10 t 1 = 2 m + 1 ( * ) 9 t 1 2 = 2 m + 1 ( * * ) .
Từ (*) suy ra: 5 t 1 = m + 1 ⇔ m = 5 t 1 − 1 thay vào (**) ta được:
9 t 1 2 = 2 ( 5 t 1 − 1 ) + 1 ⇔ 9 t 1 2 − 10. t 1 + 1 = 0 ⇔ t 1 = 1 9 ⇒ m = − 4 9 t 1 = 1 ⇒ m = 4
Vậy m = 4 hoặc m = − 4 9 là những giá trị cần tìm
Chọn D
+ Điều kiện cần: Giả sử phương trình đã cho có ba nghiệm phân biệt x 1 , x 2 , x 3 lập thành một cấp số nhân.
Theo định lý Vi-ét, ta có x 1 . x 2 . x 3 = 8
Theo tính chất của cấp số nhân, ta có x 1 x 3 = x 2 2 . Suy ra ta có x 2 3 = 8 ⇔ x 2 = 2.
Với nghiệm x=2, ta có m 2 + 6 m − 7 = 0 ⇔ m = 1 m = − 7
+ Điều kiện đủ: Với m= 1 hoặc m = -7 thì m 2 + 6 m = 7 nên ta có phương trình: x 3 − 7 x 2 + 14 x − 8 = 0.
Giải phương trình này, ta được các nghiệm là 1,2,4 Hiển nhiên ba nghiệm này lập thành một cấp số nhân với công bôị q=2
Vậy m= 1 và m= -7 là các giá trị cần tìm.
Chọn đáp án D
Phương pháp
Cho ba số a, b, c lập thành CSN thì ta có: b 2 = a c .
Cách giải
Ta có: ( x - 1 ) ( x - 3 ) ( x - m ) = 0
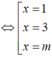
Phương trình đã cho có 3 nghiệm phân biệt
+) Giả sử 1; 3; m lập thành 1 CSN tăng
+) Giả sử m; 1; 3 lập thành 1 CSN tăng
+) Giả sử 1; m; 3 lập thành 1 CSN tăng
Vậy có 3 giá trị m thỏa mãn
Chọn C.
Đặt t = x2.
Khi đó ta có phương trình: t2 – 2(m + 1)t + 2m + 1 = 0
Phương trình đã cho có nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt
+ Với điều kiện trên thì phương trình (*) có hai nghiệm dương phân biệt là t1; t2.
Khi đó phương trình đã cho có bốn nghiệm phân biệt là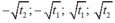
.
Bốn nghiệm này lập thành một cấp số cộng khi
Theo định lý Vi-ét ta có: t1 + t2 = 2(m + 1) ; t1.t2 = 2m + 1.
Suy ra ta có hệ phương trình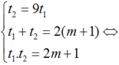
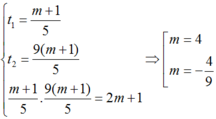
Chỉ có m = 4 thỏa mãn điều kiện .
Do đó 43 = 64.