Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đoạn sau là x2-ax-1/(2a2)=0 nha, viết thiếu.
@nguyenthanhtuan cái này là chứng minh mà bạn.

tu dpcm ap dung bdt cau-chy suy ra (bc)^2 >=(2+can2):2 , roi ban xet cai nghiem do denta >0 . ap dung vao cai vua cm o tren thi ra dieu phai cm

Theo hệ thức Vi - ét
=> a+ b = - m và a.b = 1
b + c= - n và b.c = 2
Ta có : m .n = (-m). (-n) = (a+b). (b +c)
= [(b - a) + 2a)]. [(b- c) + 2c)] = (b - a).( b - c) + 2c( b - a) + 2a.( b - c) + 4ac
= (b - a).( b - c) + 2bc - 2ac + 2ab - 2ac + 4ac
= (b - a).( b - c) + 2.2 + 2.1 = (b - a).( b - c) + 6
=> (b - a).( b - c) =m.n - 6 (ĐPCM)

Vì a, b là 2 nghiệm của phương trình x 2 + mx + 1 = 0 nên theo định lí Vi-et ta có:
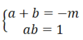
Vì b,c là 2 nghiệm của phương trình x 2 + nx + 2 = 0 nên theo định lí Vi-et ta có:
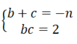
Khi đó:
(b – a)(b – c) = b 2 – bc – ab + ac
= b 2 + bc + ab + ac – 2(ab + bc)
= b( b + c) + a (b + c) – 2 (ab + bc)
= (b + c )( b + a) – 2 (ab + bc)
= (-n).(-m) – 2(1 + 2)
= nm – 6

vì b,c là nghiệm của phương trình nên \(\hept{\begin{cases}b^2-ab-\frac{1}{2a^2}=0\\c^2-ab-\frac{1}{2a^2}=0\end{cases}}\Leftrightarrow\hept{\begin{cases}b^4=\left(ab+\frac{1}{2a^2}\right)^2\\c^4=\left(ac+\frac{1}{2a^2}\right)^2\end{cases}}\)
\(b^4+c^4=\left(ab+\frac{1}{2a^2}\right)^2+\left(ac+\frac{1}{2a^2}\right)^2\ge\frac{1}{2}\left(ab+ac+\frac{1}{a^2}\right)^2\)
\(=\frac{1}{2}\left[a\left(b+c\right)+\frac{1}{a^2}\right]^2\)
mà theo viet : (tính delta đầu tiên nhá ): b+c=a.
\(\Rightarrow b^4+c^4\ge\frac{1}{2}\left(a^2+\frac{1}{a^2}\right)^2\ge2\)(AM-GM)
Dấu = xảy ra khi a=1 hoặc a=-1
^^ Lời giải hay