
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Trên google á nhưng mình thi thì đa số là nó nâng cao lên rất nhiều so với sgk, vd trong sách học là 1 + 2 = ? thì trong đây là 1 + 2 - 3 + 4 + 223 = ? nói chung là vio lớp 7 nó chỉ có nâng cao lên thôi

\(f\left(-1\right)=\left(-1\right)^2+1=1+1=2\Rightarrow B\) đúng

\(72.\)
Xét tam giác AHC vuông tại H ta có:
\(\sin C=\dfrac{AH}{AC}\) (Tỉ số lượng giác).
\(\Rightarrow\sin30^o=\dfrac{AH}{40}.\Rightarrow AH=20.\)
Xét tam giác AHB vuông tại H:
\(AB^2=AH^2+BH^2\left(Pytago\right).\)
\(\Rightarrow29^2=20^2+BH^2.\\ \Leftrightarrow BH^2=29^2-20^2.\\ \Rightarrow BH=21.\)

Bài 8:
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó:ΔABM=ΔACM
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: ME=MF
hay ΔMEF cân tại M

Bởi vì bạn trả lời có thể có nhiều từ bị sai trong câu trả lời của bạn hoặc câu trả lời của bạn có thể ko đầy đủ
Mình trả lời đúng, được chính chủ câu tk lên điểm mà? Nhưng ở điểm hỏi đáp vẫn giậm chân tại chỗ =_=


\(B=\dfrac{2008}{1}+\dfrac{2007}{2}+\dfrac{2006}{3}+...+\dfrac{2}{2007}+\dfrac{1}{2008}\)
\(=\left(1+\dfrac{2007}{2}\right)+\left(1+\dfrac{2006}{3}\right)+...+\left(\dfrac{2}{1007}+1\right)+\left(\dfrac{1}{2008}+1\right)+1\)
\(=\dfrac{2009}{1}+\dfrac{2009}{2}+...+\dfrac{2009}{2008}\)
\(=2009\)



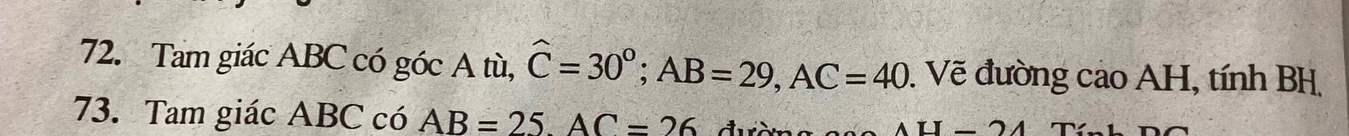 bài 72 giúp em 🥲🥲
bài 72 giúp em 🥲🥲


a: Xét ΔAMB và ΔAMC có
AB=AC
AM chung
MB=MC
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là tia phân giác
c: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
d: Xét ΔAKB và ΔAKC có
AK chung
\(\widehat{BAK}=\widehat{CAK}\)
AB=AC
Do đó: ΔAKB=ΔAKC
Suy ra: KB=KC