
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bài 1:
\(\left\{{}\begin{matrix}x+y=57\\4x-2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+4y=228\\4x-2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6y=234\\x+y=57\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=39\\x=18\end{matrix}\right.\)

a: \(\Leftrightarrow\left\{{}\begin{matrix}3x+6y=4\\x+4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{3}\\x=\dfrac{2}{3}\end{matrix}\right.\)

a: \(\left\{{}\begin{matrix}3x+6y=4\\x+4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+6y=4\\3x+12y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{3}\\x=2-\dfrac{4}{3}=\dfrac{2}{3}\end{matrix}\right.\)

a: góc OBA+góc OCA=180 độ
=>ABOC nội tiếp
b: Xét ΔABE và ΔADB có
góc ABE=góc ADB
góc BAE chung
=>ΔABE đồng dạng với ΔADB
=>AB/AD=AE/AB
=>AB^2=AD*AE

a, Vì DM//AB nên ADMB là hình thang
Mà ADMB nội tiếp (O) nên ADMB là htc
Do đó \(BM=AD\Rightarrow\stackrel\frown{BM}=\stackrel\frown{AD}\)
b, Xét (O) có \(\widehat{AMD}=\widehat{AND}\) (cùng chắn AD)
Vì AM//BN nên \(\widehat{AMN}=\widehat{MNB}\)
\(\Rightarrow\widehat{AMD}+\widehat{AMN}+\widehat{DNM}=\widehat{AND}+\widehat{MNB}+\widehat{DNM}\\ \Rightarrow\widehat{NDM}=\widehat{ANB}=90^0\\ \Rightarrow DM\perp DN\\ \Rightarrow DN\perp AB\left(DM//AB\right)\)
c, Kẻ EC//AM(C∈DM)
Gọi \(AM\cap DE=I\)
Vì EC//AM nên EC//ID
\(\Rightarrow\widehat{DIM}=\widehat{DEC}\\ \Rightarrow90^0-\widehat{DIM}=90^0-\widehat{DEC}\\ \Rightarrow\widehat{DMI}=\widehat{CEB}\)
Cmtt ta được \(\widehat{DIM}=\widehat{ECB}\)
\(\Rightarrow\Delta DIM\sim\Delta BCE\left(g.g\right)\\ \Rightarrow\widehat{IDM}=\widehat{EBC}=90^0\\ \Rightarrow BC\perp AB\Rightarrow BC//EN\)
Mà EC//AM//BN nên ECBN là hbh
\(\Rightarrow BC=EN\)
Vì CD//BE và DE//BC nên BCDE là hbh
\(\Rightarrow BC=DE\)
Vậy \(EN=DE\)

1)
ĐKXĐ: x>4
Ta có: \(\dfrac{\sqrt{x+5}}{\sqrt{x-4}}=\dfrac{\sqrt{x-2}}{\sqrt{x+3}}\)
\(\Leftrightarrow x^2+8x+15=x^2-6x+8\)
\(\Leftrightarrow8x+6x=8-15\)
\(\Leftrightarrow14x=-7\)
hay \(x=-\dfrac{1}{2}\)(loại)
2) Ta có: \(\sqrt{4x^2-9}=3\sqrt{2x-3}\)
\(\Leftrightarrow\sqrt{2x-3}\left(\sqrt{2x+3}-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\2x+3=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=3\\2x=6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=3\end{matrix}\right.\)

3:
1: Thay x=3+2căn 2 vào B, ta được:
\(B=\dfrac{3+2\sqrt{2}+12}{\sqrt{2}+1-1}=\dfrac{15+2\sqrt{2}}{\sqrt{2}}=\dfrac{15\sqrt{2}+4}{2}\)
2:
\(A=\dfrac{\sqrt{x}-2-4\sqrt{x}-8+x+12}{x-4}=\dfrac{x-3\sqrt{x}+2}{x-4}\)
\(=\dfrac{\left(\sqrt{x}-2\right)\cdot\left(\sqrt{x}-1\right)}{x-4}=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)
\(P=A\cdot B=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\cdot\dfrac{x+2}{\sqrt{x}-1}=\dfrac{x+2}{\sqrt{x}+2}\)
\(=\dfrac{x-4+6}{\sqrt{x}+2}\)
\(=\sqrt{x}-2+\dfrac{6}{\sqrt{x}+2}\)
\(=\sqrt{x}+2+\dfrac{6}{\sqrt{x}+2}-4\)
=>\(P>=2\sqrt{\left(\sqrt{x}+2\right)\cdot\dfrac{6}{\sqrt{x}+2}}-4=2\sqrt{6}=-4\)
Dấu = xảy ra khi (căn x+2)^2=6
=>căn x+2=căn 6
=>căn x=căn 6-2
=>x=10-4*căn 6







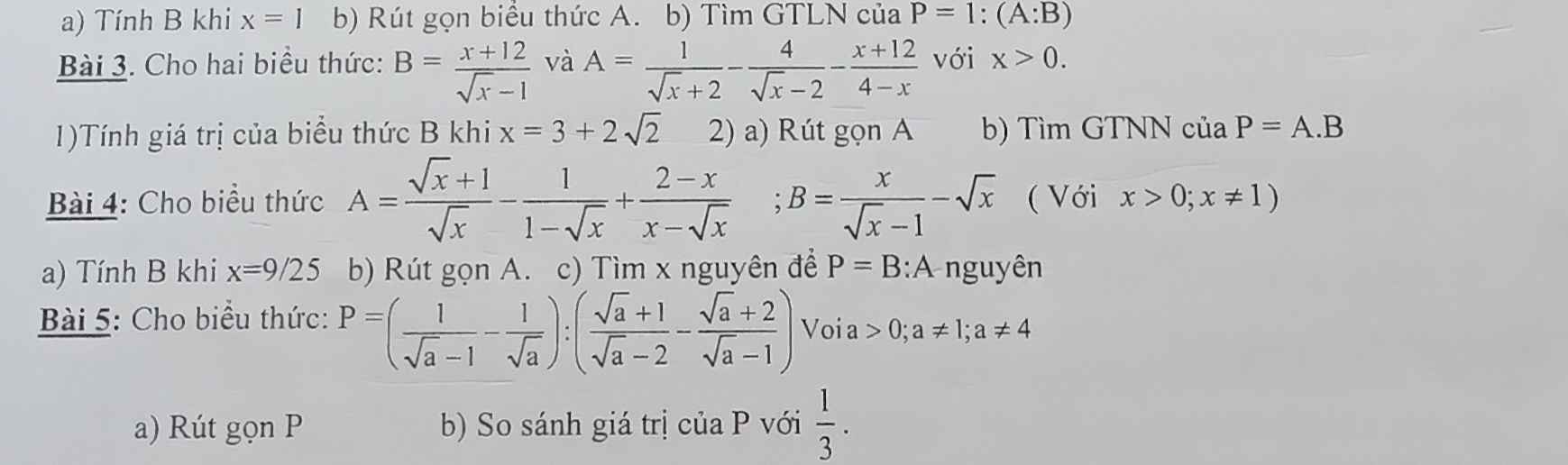
a: \(\Leftrightarrow\left\{{}\begin{matrix}3x+6y=4\\x+4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{3}\\x=\dfrac{2}{3}\end{matrix}\right.\)