
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1)
ĐKXĐ: x>4
Ta có: \(\dfrac{\sqrt{x+5}}{\sqrt{x-4}}=\dfrac{\sqrt{x-2}}{\sqrt{x+3}}\)
\(\Leftrightarrow x^2+8x+15=x^2-6x+8\)
\(\Leftrightarrow8x+6x=8-15\)
\(\Leftrightarrow14x=-7\)
hay \(x=-\dfrac{1}{2}\)(loại)
2) Ta có: \(\sqrt{4x^2-9}=3\sqrt{2x-3}\)
\(\Leftrightarrow\sqrt{2x-3}\left(\sqrt{2x+3}-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\2x+3=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=3\\2x=6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=3\end{matrix}\right.\)

a: góc OBA+góc OCA=180 độ
=>ABOC nội tiếp
b: Xét ΔABE và ΔADB có
góc ABE=góc ADB
góc BAE chung
=>ΔABE đồng dạng với ΔADB
=>AB/AD=AE/AB
=>AB^2=AD*AE

a: \(\Leftrightarrow\left\{{}\begin{matrix}3x+6y=4\\x+4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{3}\\x=\dfrac{2}{3}\end{matrix}\right.\)

Ta có: \(-3x^2-5x-2=0\)
Theo định lý vi-et ta có:
\(x_1+x_2=-\dfrac{b}{a}=-\dfrac{-5}{-3}=-\dfrac{5}{3}\)
\(x_1x_2=\dfrac{c}{a}=\dfrac{-2}{-3}=\dfrac{2}{3}\)
a) \(M=x_1+\dfrac{1}{x_1}+\dfrac{1}{x_2}+x_2\)
\(M=\left(x_1+x_2\right)+\dfrac{x_1+x_2}{x_1x_2}\)
\(M=-\dfrac{5}{3}+\dfrac{-\dfrac{5}{3}}{\dfrac{2}{3}}=-\dfrac{25}{6}\)
b) \(N=\dfrac{1}{x_1+3}+\dfrac{1}{x_2+3}\)
\(N=\dfrac{x_2+3+x_1+3}{\left(x_1+3\right)\left(x_2+3\right)}\)
\(N=\dfrac{\left(x_1+x_2\right)+6}{x_1x_2+3\left(x_1+x_2\right)+9}\)
\(N=\dfrac{-\dfrac{5}{3}+6}{\dfrac{2}{3}+3\cdot-\dfrac{5}{3}+9}=\dfrac{13}{14}\)
c) \(P=\dfrac{x_1-3}{x^2_1}+\dfrac{x_2-3}{x^2_2}\)
\(P=\dfrac{x^2_2\left(x_1-3\right)+x^2_1\left(x_2-3\right)}{x^2_1x^2_2}\)
\(P=\dfrac{x^2_2x_1+x^2_1x_2-3x^2_2-3x^2_1}{\left(x_1x_2\right)^2}\)
\(P=\dfrac{x_1x_2\left(x_1+x_2\right)-3\left[\left(x_1+x_2\right)^2-2x_1x_2\right]}{\left(x_1x_2\right)^2}\)
\(P=\dfrac{\dfrac{2}{3}\cdot-\dfrac{5}{3}-3\cdot\left[\left(-\dfrac{5}{3}\right)^2-2\cdot\dfrac{2}{3}\right]}{\left(\dfrac{2}{3}\right)^2}=-\dfrac{49}{4}\)
d) \(Q=\dfrac{x_1}{x_2+2}+\dfrac{x_2}{x_1+2}\)
\(Q=\dfrac{x_1\left(x_1+2\right)+x_2\left(x_2+2\right)}{\left(x_2+2\right)\left(x_1+2\right)}\)
\(Q=\dfrac{x^2_1+2x_1+x_2^2+2x_2}{x_1x_2+2x_2+2x_1+4}\)
\(Q=\dfrac{\left(x^2_1+x^2_2\right)+2\left(x_1+x_2\right)}{x_1x_2+2\left(x_1+x_2\right)+4}\)
\(Q=\dfrac{\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)}{x_1x_2+2\left(x_1+x_2\right)+4}\)
\(Q=\dfrac{\left(-\dfrac{5}{3}\right)^2-2\cdot\dfrac{2}{3}+2\cdot-\dfrac{5}{3}}{\dfrac{2}{3}+2\cdot-\dfrac{5}{3}+4}=-\dfrac{17}{12}\)

Lời giải:
a. Xét tứ giác $ADHE$ có $\widehat{A}=\widehat{D}=\widehat{E}=90^0$ nên là hcn
$\Rightarrow AH=DE$
$\Rightarrow DE.BC=AH.BC=2S_{ABC}=AB.AC$ (đpcm)
b.
Xét tam giác vuông $ADH$ vuông tại $D$ thì:
$\frac{AD}{AH}=\cos \widehat{DAH}=\cos (90^0-\widehat{HAC})=\cos C$
$\Rightarrow AD=AH\cos C$

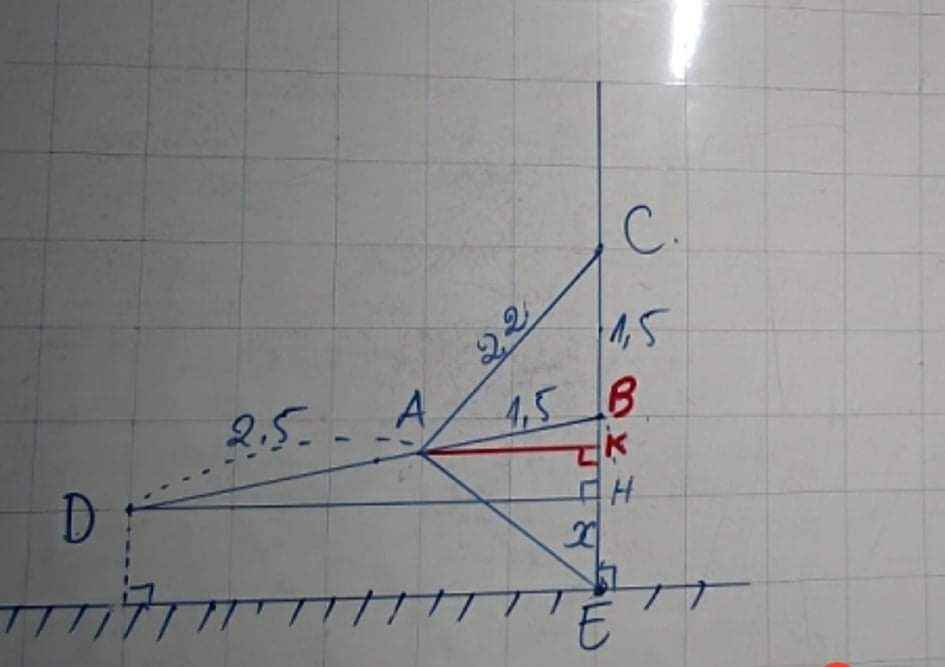
Gọi DH là khoảng cách thấp nhất từ máy bay đến mặt đất, khi đó AC có độ dài lớn nhất là 2,2m. Dựng hình chữ nhật DHEK => DH = EK
Do BA = BE = BC = 1,5m cố định nên tam giác ACE vuông tại A
Xét tam giác ACE vuông tại A có cos\(\widehat{ECA}\) = \(\dfrac{CA}{CE}=\dfrac{2,2}{3}\) => \(\widehat{ECA}\) \(\approx\) 42o50'
BA = BC => tam giác ABC cân tại B => \(\widehat{BAC}=\widehat{BCA}\) = \(\widehat{ECA}\) \(\approx\) 42o50'
=> \(\widehat{DBK}\) = \(\widehat{BAC}+\widehat{BCA}\) = 2.\(\widehat{BCA}\) = 85o40'
Xét tam giác DBK vuông tại D có: BK = BD. cos\(\widehat{DBK}\)
= 4.cos85o40' \(\approx\) 0,3022
=> DH = KE \(\approx\) 1,5 - 0,3022 \(\approx\)1,2 (m)




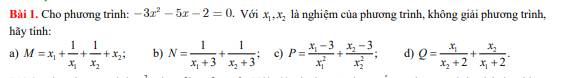


12B
13B
14C
15D
16A
17C
18D
19C
20D
21C
22C
23D