Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) ở bài này bạn áp dụng hằng đẳng thức :\(a^2-b^2=\left(a-b\right)\left(a+b\right)\)
\(\sqrt{137^2-88^2}\)
\(=\sqrt{\left(137-88\right)\left(137+88\right)}\)
\(=\sqrt{49.225}\)
\(=\sqrt{49}.\sqrt{225}\)
\(=7.15\)
\(=105\)
2) bài này cũng giống bài 1 cũng áp dụng hằng đẳng thức :\(a^2-b^2=\left(a-b\right)\left(a+b\right)\)
\(\sqrt{192^2-111^2}\)
\(=\sqrt{\left(192-111\right)\left(192+111\right)}\)
\(=\sqrt{81.303}\)
\(=9\sqrt{303}\)
P/s : do số 303 là số chính phương nên ko thể phá căn được

Bạn Nguyễn Tiến Đạt trình quá nên tớ kh dám nói gì thêm :v

\(\sqrt{137^2-88^2}\)
Sử dụng hằng đẳng thức ta được:
\(\sqrt{\left(137-88\right)\left(137+88\right)}\)
= \(\sqrt{49.225}\)
= \(\sqrt{7^2.15^2}\)
Sử dụng quy tắc khai phương ta được
\(7.15\)= 105
Chúc bạn học tốt ^^

\(A=\sqrt{3+\sqrt{5}}.\sqrt{3-\sqrt{5}}=\sqrt{3^2-\left(\sqrt{5}\right)^2}=\sqrt{4}=2\)
\(B=\sqrt{150.27.96}=\sqrt{150}.\sqrt{27}.\sqrt{96}=5\sqrt{6}.3\sqrt{3}.4\sqrt{6}=360\sqrt{3}\)
\(C=\left(\sqrt{27}+\sqrt{48}\right)^2-\left(\sqrt{27}-\sqrt{48}\right)^2\)\(=\left[\left(\sqrt{27}+\sqrt{48}-\sqrt{27}+\sqrt{48}\right)\left(\sqrt{27}+\sqrt{48}+\sqrt{27}-\sqrt{48}\right)\right]\)
\(=2\sqrt{27}.2\sqrt{48}=2.3\sqrt{3}.2.4\sqrt{3}=144\)
\(D=\sqrt{137^2-88^2}-\sqrt{192^2-111^2}=\sqrt{\left(137+88\right)\left(137-88\right)}-\sqrt{\left(192+111\right)\left(192-111\right)}\)
\(=\sqrt{225.49}-\sqrt{303.81}=15.7-9.\sqrt{303}=9\left(\frac{35}{3}-\sqrt{303}\right)\)
\(E=\sqrt{\frac{225}{4}.\frac{81}{25}.\frac{49}{64}}=\frac{15}{2}.\frac{9}{5}.\frac{7}{8}=\frac{189}{16}\)
\(F=\sqrt{\frac{27}{25}}.\sqrt{\frac{49}{189}}.\sqrt{\frac{700}{99}}=\frac{3\sqrt{3}}{5}.\frac{7}{3\sqrt{21`}}.\frac{10\sqrt{7}}{3\sqrt{11}}=\frac{14}{3\sqrt{11}}\)
\(H=\sqrt{105}.\left[\sqrt{\frac{15}{7}}-\sqrt{\frac{35}{5}}+\sqrt{\frac{21}{5}}\right]=\sqrt{105}.\left[\sqrt{\frac{15}{7}}-\sqrt{7}+\sqrt{\frac{21}{5}}\right]\)
\(=\sqrt{105}.\left[\frac{\sqrt{75}-\sqrt{49}+\sqrt{147}}{\sqrt{35}}\right]=\sqrt{3}\left(12\sqrt{3}-7\right)=36-7\sqrt{3}\)
\(K=\sqrt{64.14.21.54}-\sqrt{35.45.12}=8.\sqrt{14}.\sqrt{21}.3\sqrt{6}-\sqrt{35}.3\sqrt{5}.2\sqrt{3}\)
\(=24.\sqrt{14.21.6}-6\sqrt{35.5.3}=24.42-30\sqrt{21}=30\left(\frac{168}{5}-\sqrt{21}\right)\)

1.
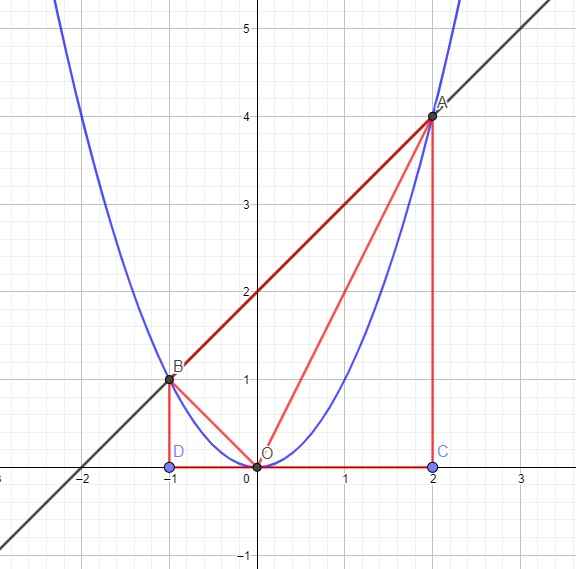
Dễ dàng tìm được tọa độ 2 giao điểm, do vai trò của A, B như nhau, giả sử \(A\left(2;4\right)\) và \(B\left(-1;1\right)\)
Gọi C và D lần lượt là 2 điểm trên trục Ox có cùng hoành độ với A và B, hay \(C\left(2;0\right)\) và \(D\left(-1;0\right)\)
Khi đó ta có ABDC là hình thang vuông tại D và C, các tam giác OBD vuông tại D và tam giác OAC vuông tại C
Độ dài các cạnh: \(BD=\left|y_B\right|=1\) ; \(AC=\left|y_A\right|=4\)
\(OD=\left|x_D\right|=1\) ; \(OC=\left|x_C\right|=2\) ; \(CD=\left|x_C-x_D\right|=3\)
Ta có:
\(S_{OAB}=S_{ABDC}-\left(S_{OBD}+S_{OAC}\right)\)
\(=\dfrac{1}{2}CD.\left(AC+BD\right)-\left(\dfrac{1}{2}BD.OD+\dfrac{1}{2}AC.OC\right)\)
\(=\dfrac{1}{2}.3.\left(4+1\right)-\left(\dfrac{1}{2}.1.1+\dfrac{1}{2}.4.2\right)=3\)


câu 1:
đường thẳng (d) song song với đường thẳng y=3x+1 khi a=3
vậy hệ số góc của đường thẳng (d) song song với đường thẳng y=3x+1 là 3
câu 2:
vì góc tạo bởi đường thẳng (d):y=ax+b(a≠0) với trục Ox là 30o nên
\(a=\tan30^o=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)
vậy hệ số góc của đường thẳng (d) tạo với trục Ox là\(\dfrac{\sqrt{3}}{3}\)


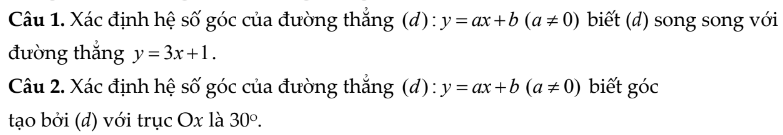
Tokoyami bn đăng từng câu 1 thôi. Nhiều thế này thì ko đủ kiên nhẫn để làm đâu
bạn này đang đau khổ