K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
31 tháng 8 2021
đề đâu, mà giải chi tiết thì đăng 1 câu hỏi trong 1 lần đăng thôi
31 tháng 8 2021
\(a,x^3+9x^2+27x+27=\left(x+3\right)^3\\ b,\dfrac{x^3}{8}+\dfrac{3}{4}x^2y^2+\dfrac{3}{2}xy^4+y^6=\left(\dfrac{x}{2}+y^2\right)^3\\ c,x^3+6x^2+12x+8=\left(x+2\right)^3\\ d,27x^3-54x^2y+36xy^2-8y^3=\left(3x-2y\right)^3\\ e,8x^6-12x^4+6x^2-1=\left(2x^2-1\right)^3\)
XD
2
28 tháng 10 2021
2
a) \(=x\left(3x^3-x^2+5\right)\)
b) \(=\left(2x+3y\right)\left(x-y\right)\)
c) \(=\left(x^2-3x\right)-\left(4x-12\right)=x\left(x-3\right)-4\left(x-3\right)=\left(x-3\right)\left(x-4\right)\)
LN
28 tháng 10 2021
a, = x.(3x3 - x2 + 5)
b, = 2x.(x - y) + 3y.(x - y) = (x - y).(2x + 3y)
c, = x2 - 3x - 4x + 12 = (x2 - 3x) - (4x - 12) = x.(x - 3) - 4.(x - 3) = (x - 3).(x - 4)
2 tháng 3 2023
a: \(CB=\sqrt{8^2+6^2}=10\left(cm\right)\)
Xet ΔBAC có CD là phân giác
nên AD/AC=BD/CB
=>AD/3=BD/5=(AD+DB)/(3+5)=8/8=1
=>AD=3cm; BD=5cm
b: Xét ΔABC vuông tại A có AF là đường cao
nên AB^2=BF*BC
\(BF=\dfrac{8^2}{10}=6.4\left(cm\right)\)
CF=10-6,4=3,6cm
IF/AI=BF/BA
AD/DB=AC/CB
mà BF/BA=AC/CB
nên IF/AI=AD/DB
b: Xét ΔHDB vuông tạiH và ΔFCA vuông tại F có
góc HBD=góc FAC
=>ΔHDB đồng dạng với ΔFCA
26 tháng 9 2021
Gọi K là trung điểm của DC
Suy ra: AD=DK=KC
Xét ΔDBC có
M là trung điểm của BC
K là trung điểm của CD
Do đó: MK là đường trung bình của ΔDBC
Suy ra: MK//BD
Xét ΔAMK có
D là trung điểm của AK
DI//MK
Do đó: I là trung điểm của AM
hay AI=IM
18 tháng 11 2021
\(9,\dfrac{x^2-81}{10x^2-90x}=\dfrac{\left(x-9\right)\left(x+9\right)}{10x\left(x-9\right)}=\dfrac{x+9}{10x}\Rightarrow M=10x\\ 10,\dfrac{2x^2+3x}{4x^2-9}=\dfrac{x\left(2x+3\right)}{\left(2x-3\right)\left(2x+3\right)}=\dfrac{x}{2x-3}\Rightarrow A=x\)
18 tháng 11 2021
\(9,M=\dfrac{\left(x+9\right)\left(10x^2-90x\right)}{x^2-81}=\dfrac{10x\left(x+9\right)\left(x-9\right)}{\left(x-9\right)\left(x+9\right)}=10x\\ 10,A=\dfrac{\left(2x-3\right)\left(2x^2+3x\right)}{4x^2-9}=\dfrac{x\left(2x+3\right)\left(2x-3\right)}{\left(2x-3\right)\left(2x+3\right)}=x\)
30 tháng 8 2021
e) \(\left(x^2-4\right)\left(x^2+4\right)=\left(x^2\right)^2-4^2=x^4-16\)
f) \(\left(x+y\right)^2+\left(x-y\right)^2=x^2+2xy+y^2+x^2-2xy+y^2=2x^2+2y^2\)
KK
30 tháng 8 2021
(x2 - 4)(x2 + 4)
Áp dụng hằng đẳng thức số 3, ta có:
<=> \(\left[\left(x^2\right)^2-4^2\right]\)
<=> (x4 - 16)
Mik làm chi tiết rồi, có gì ko hiểu bảo mik
NN
1
PL
0
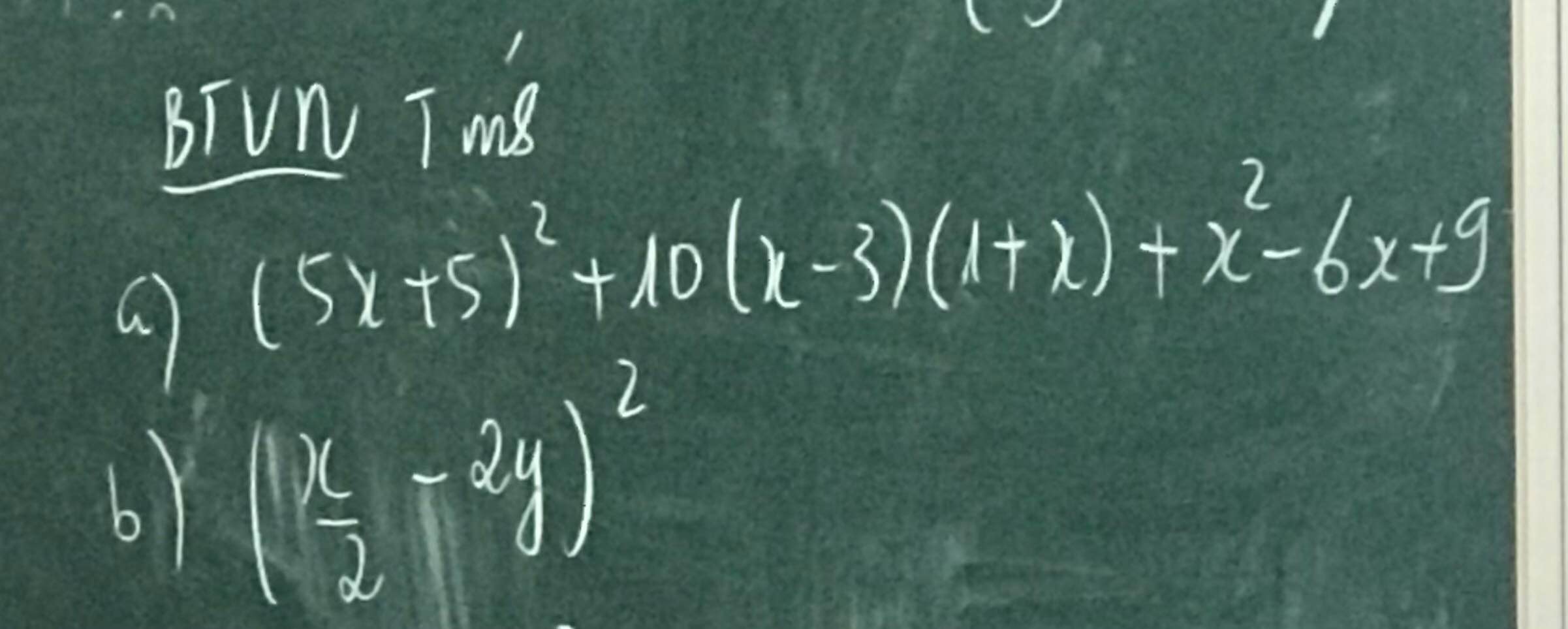
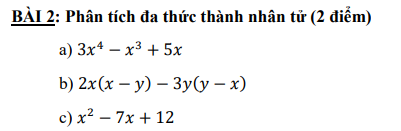
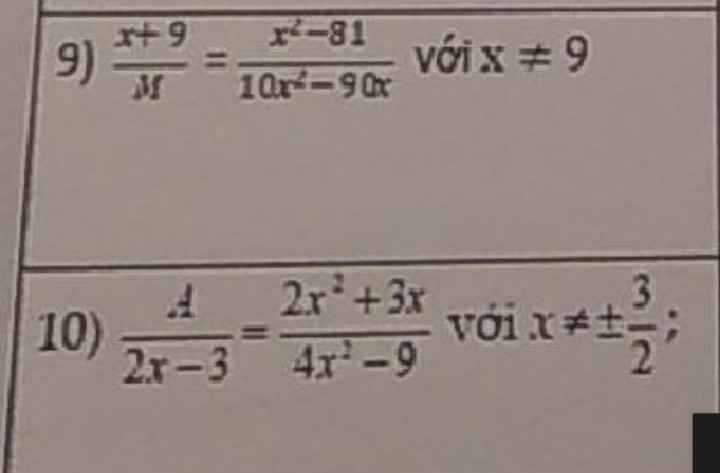
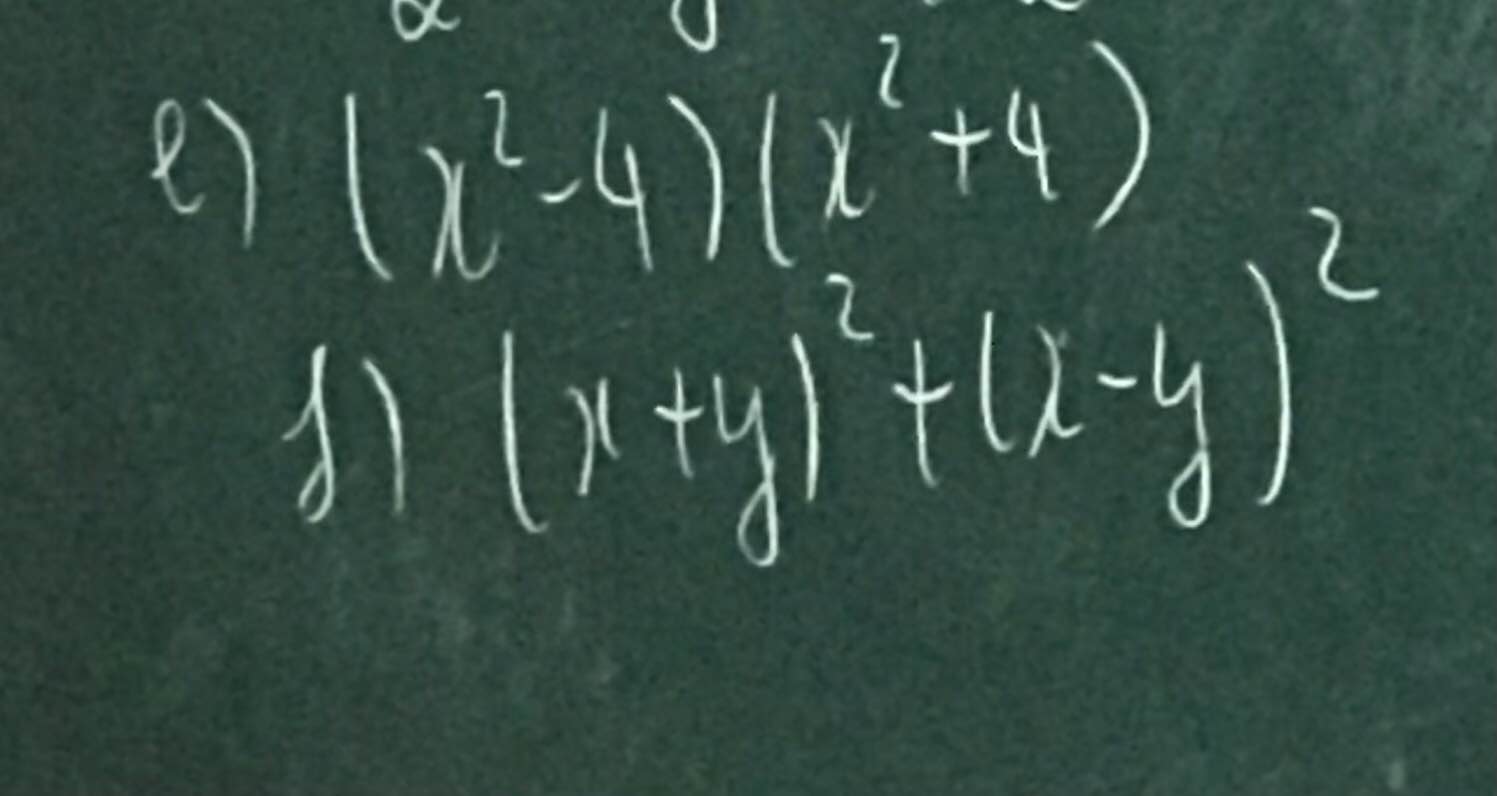
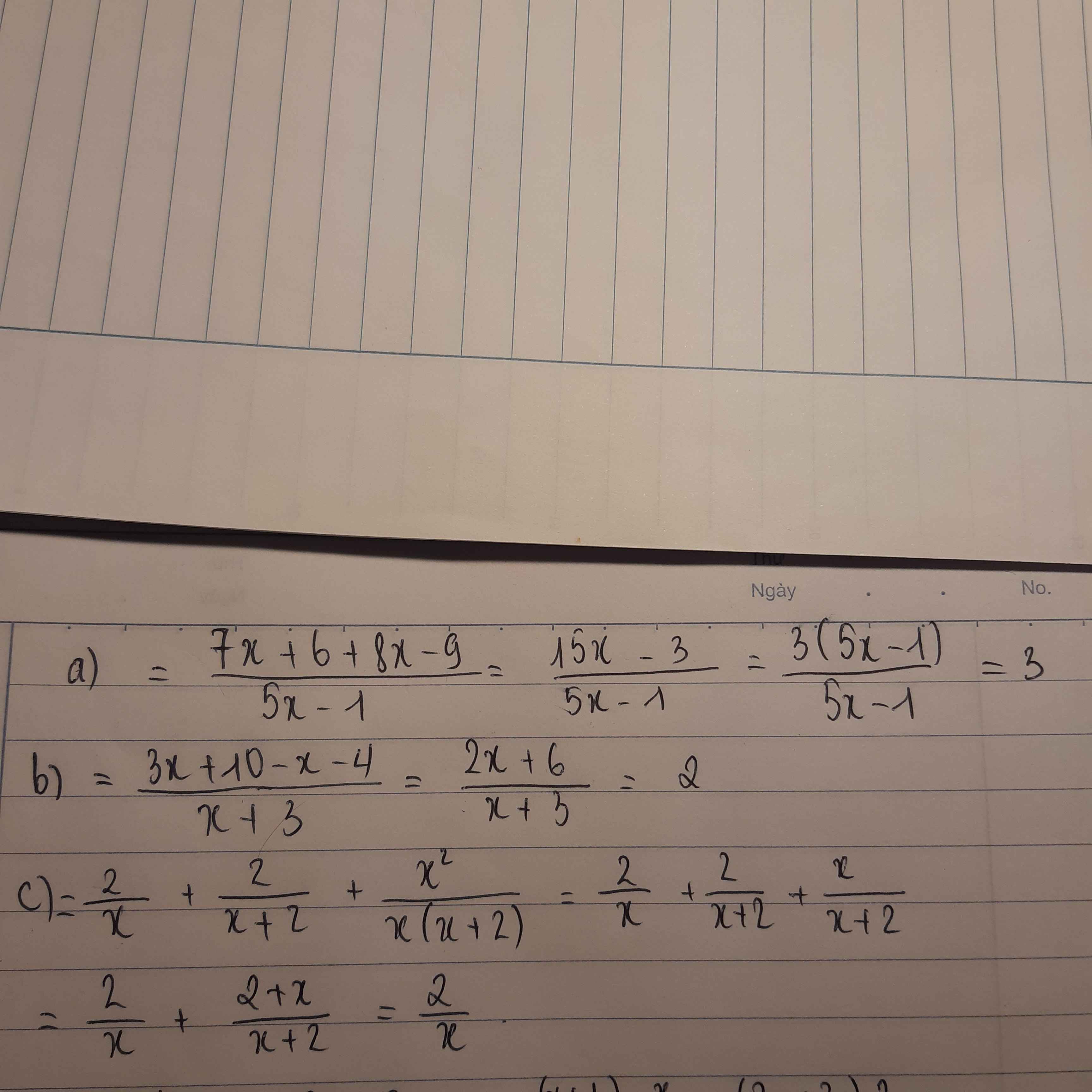
a) \(\left(5x+5\right)^2+10\left(x-3\right)\left(1+x\right)+x^2-6x+9=\left[5\left(x+1\right)\right]^2+2.5\left(x+1\right)\left(x-3\right)+\left(x-3\right)^2=\left[5\left(x+1\right)+\left(x-3\right)\right]^2=\left(5x+5+x-3\right)^2=\left(6x+2\right)^2=\left(6x\right)^2+2.6x.2+2^2=36x^2+24x+4\)
b) \(\left(\dfrac{x}{2}-2y\right)^2=\left(\dfrac{x}{2}\right)^2-2.\dfrac{x}{2}.2y+\left(2y\right)^2=\dfrac{x^2}{4}-2xy+4y^2\)
a: \(\left(5x+5\right)^2+10\left(x-3\right)\left(x+1\right)+x^2-6x+9\)
\(=\left[5\left(x+1\right)\right]^2+2\cdot5\left(x+1\right)\cdot\left(x-3\right)+\left(x-3\right)^2\)
\(=\left(5x+5+x-3\right)^2\)
\(=\left(6x+2\right)^2\)
b: \(\left(\dfrac{1}{2}x-2y\right)^2=\dfrac{1}{4}x^2-2xy+4y^2\)