K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 9 2023
Vậy \(( - 32{x^5} + 1):( - 2x + 1) = 16{x^4} + 8{x^3} + 4{x^2} + 2x + 1\).
EC
16 tháng 8 2016
Câu 1:
a)A=|x+1|+2016
Vì |x+1|\(\ge\)0
Suy ra:|x+1|+2016\(\ge\)2016
Dấu = xảy ra khi x+1=0
x=-1
Vậy MinA=2016 khi x=-1
b)B=2017-|2x-\(\frac{1}{3}\)|
Vì -|2x-\(\frac{1}{3}\)|\(\le\)0
Suy ra:2017-|2x-\(\frac{1}{3}\)|\(\le\)2017
Dấu = xảy ra khi \(2x-\frac{1}{3}=0\)
\(2x=\frac{1}{3}\)
\(x=\frac{1}{6}\)
Vậy Max B=2017 khi \(x=\frac{1}{6}\)
c)C=|x+1|+|y+2|+2016
Vì |x+1|\(\ge\)0
|y+2|\(\ge\)0
Suy ra:|x+1|+|y+2|+2016\(\ge\)2016
Dấu = xảy ra khi x+1=0;x=-1
y+2=0;y=-2
Vậy MinC=2016 khi x=-1;y=-1
d)D=-|x+\(\frac{1}{2}\)|-|y-1|+10
=10-|x+\(\frac{1}{2}\)|-|y-1|
Vì -|x+\(\frac{1}{2}\)|\(\le\)0
-|y-1| \(\le\)0
Suy ra: 10-|x+\(\frac{1}{2}\)|-|y-1| \(\le\)10
Dấu = xảy ra khi \(x+\frac{1}{2}=0;x=-\frac{1}{2}\)
y-1=0;y=1
Vậy Max D=10 khi x=\(-\frac{1}{2}\);y=1
16 tháng 8 2016
Bài 1:
a)Ta thấy: \(\left|x+1\right|\ge0\)
\(\Rightarrow\left|x+1\right|+2016\ge0+2016=2016\)
\(\Rightarrow A\ge2016\)
Dấu = khi x=-1
Vậy MinA=2016 khi x=-1
b)Ta thấy:\(\left|2x-\frac{1}{3}\right|\ge0\)
\(\Rightarrow-\left|2x-\frac{1}{3}\right|\le0\)
\(\Rightarrow2017-\left|2x-\frac{1}{3}\right|\le2017-0=2017\)
\(\Rightarrow B\le2017\)
Dấu = khi x=1/6
Vậy Bmin=2017 khi x=1/6
c)Ta thấy:\(\begin{cases}\left|x+1\right|\\\left|y+2\right|\end{cases}\ge0\)
\(\Rightarrow\left|x+1\right|+\left|y+2\right|\ge0\)
\(\Rightarrow\left|x+1\right|+\left|y+2\right|+2016\ge0+2016=2016\)
\(\Rightarrow D\ge2016\)
Dấu = khi x=-1 và y=-2
Vậy MinD=2016 khi x=-1 và y=-2
d)Ta thấy:\(\begin{cases}-\left|x+\frac{1}{2}\right|\\-\left|y-1\right|\end{cases}\le0\)
\(\Rightarrow-\left|x+\frac{1}{2}\right|-\left|y-1\right|\le0\)
\(\Rightarrow-\left|x+\frac{1}{2}\right|-\left|y-1\right|+10\le0+10=10\)
\(\Rightarrow D\le10\)
Dấu = khi x=-1/2 và y=1
Vậy MaxD=10 khi x=-1/2 và y=1
13 tháng 3 2022
\(A=\left(x-1\right)^2+1.\\ \left(x-1\right)^2\ge0\forall x\in R.\\ 1>0.\\ \Rightarrow\left(x-1\right)^2+1\ge1\forall x\in R.\\ \Rightarrow A\ge1.\\ \Rightarrow A_{min}=1.\)
\(B=x^2+x^4-\dfrac{1}{2}.\\ x^2+x^4\ge0\forall x\in R.\\ \Leftrightarrow x^2+x^4-\dfrac{1}{2}\ge\dfrac{-1}{2}\forall x\in R.\\ \Rightarrow B\ge\dfrac{-1}{2}.\\ \Rightarrow B_{min}=\dfrac{-1}{2}.\)
\(D=\dfrac{2}{\left(x-1\right)^2}+1.\\ \left(x-1\right)^2\ge0\forall x\in R.\\ \Leftrightarrow\dfrac{2}{\left(x-1\right)^2}\ge0.\\ \Leftrightarrow\dfrac{2}{\left(x-1\right)^2}+1\ge1\forall x\in R.\\ \Rightarrow D\ge1.\\ \Rightarrow D_{min}=1.\)
29 tháng 6 2022
a: đề thiếu chỗ giá trị của y nếu x=-1 hoặc x=1/2 rồi bạn
b: Theo đề,ta có hệ phương trình:
\(\left\{{}\begin{matrix}2\cdot4+2b+c=5\\2+b+c=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2b+c=-3\\b+c=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=0\\c=-3\end{matrix}\right.\)
2 tháng 2
a: \(\left(x+\dfrac{1}{4}\right)+\left(3x-4\right)+2\left(x-3\right)=1\)
=>\(x+\dfrac{1}{4}+3x-4+2x-6=1\)
=>\(6x-\dfrac{39}{4}=1\)
=>\(6x=1+\dfrac{39}{4}=\dfrac{43}{4}\)
=>\(x=\dfrac{43}{4}:6=\dfrac{43}{24}\)
b: \(2\left(x-3\right)=3\left(x+2\right)-x+1\)
=>\(2x-6=3x+6-x+1\)
=>2x-6=2x+7
=>-6=7(vô lý)
c: \(x\left(x+3\right)+x\left(x-2\right)=2x\left(x-1\right)\)
=>\(x^2+3x+x^2-2x=2x^2-2x\)
=>3x-2x=-2x
=>3x=0
=>x=0
d: \(\left(x-1\right)\cdot3x-2\left(x+2\right)-2x=x\left(x-1\right)\)
=>\(3x^2-3x-2x-4-2x=x^2-x\)
=>\(3x^2-7x-4-x^2+x=0\)
=>\(2x^2-6x-4=0\)
=>\(x^2-3x-2=0\)
=>\(x=\dfrac{3\pm\sqrt{17}}{2}\)
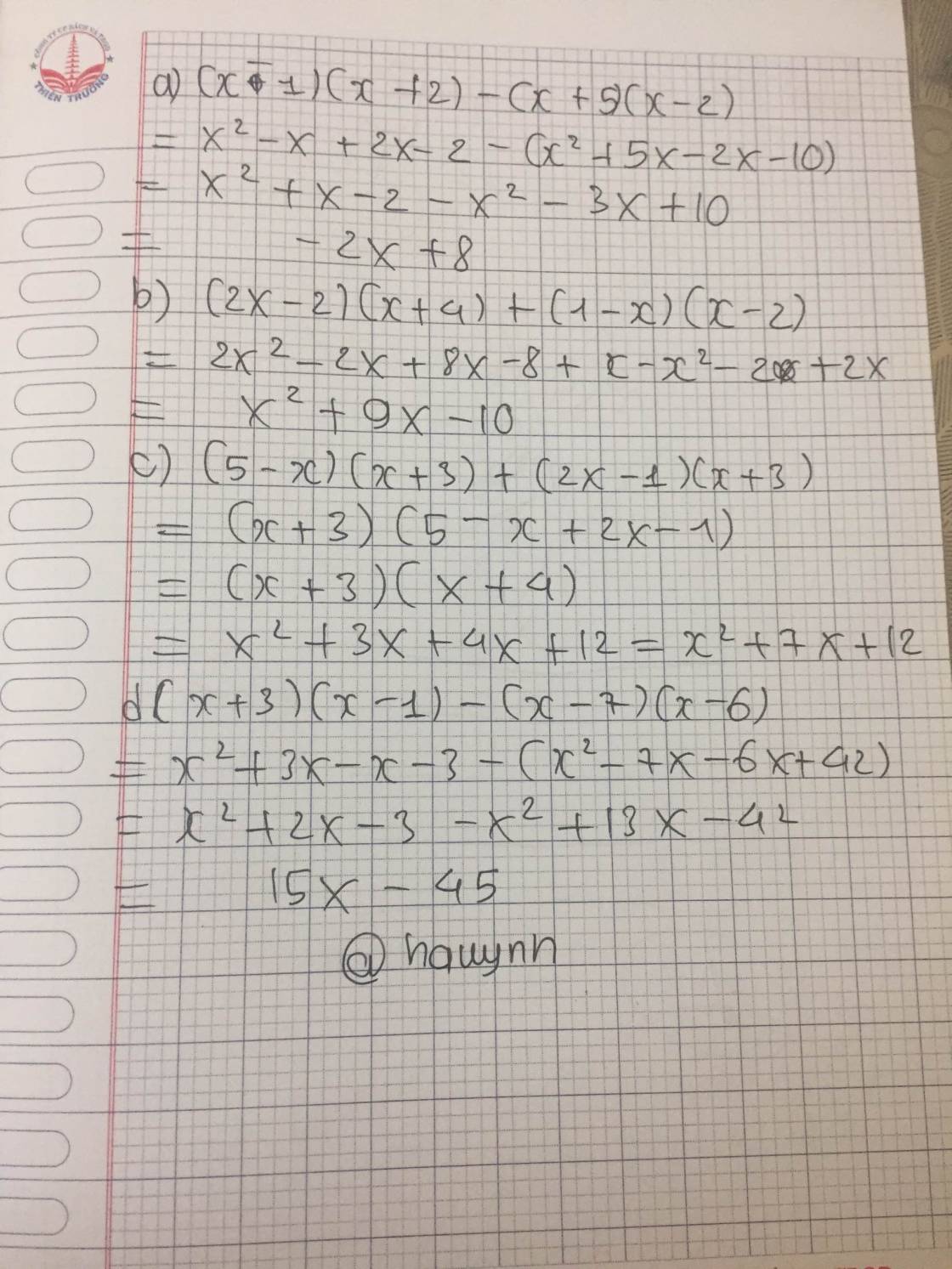
`D(x) = (x+2) (1-x)`
`D(x)= x - x + 2 -2x`
`D(x) = -2x+2`
Em cần viết đề bài rõ ràng nhé!