
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


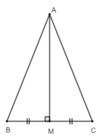
Giả sử Δ A B C có AM là trung tuyến đồng thời là đường trung trực. Ta sẽ chứng minh Δ A B C là tam giác cân. Thật vậy, vì AM là trung tuyến của Δ A B C g t ⇒ B M = M C (tính chất trung tuyến)


1: Đường trung trực là đường thẳng vuông góc với đoạn thẳng tại trung điểm của nó.
2 : Đường cao là đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện.
3 : Trong một tam giác vuông ,bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông .
1,Trung tuyến là gì?
2,Đường trung trực là gì?
3,phát biểu tiên đề ơclit?
4,Phát biểu định lí pi-ta-go?

1.trung tuyến của một tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện. Mỗi tam giác đều có ba trung tuyến. Đối với tam giác cân và tam giác đều, mỗi trung tuyến của tam giác chia đôi các góc ở đỉnh với hai cạnh kề có chiều dài bằng nhau.
2.đường trung trực của một đoạn thẳng là đường vuông góc với đoạn thẳng tạitrung điểm của đoạn thẳng đó.Trong đường tròn, giao 2 tiếp tuyến thì điểm đó đến tâm là đường trung trực.
3.Qua một điểm nằm ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
4.Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
1. Là: Khu vực nối liền giữa hậu phương và tiền tuyến.
2. Là: Đường thẳng vuông góc với một đoạn thẳng tại điểm giữa của đoạn ấy.
3.
1. Tiên đề ơclit
Qua một điểm nằm ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
2. Tính chất của hai đường thẳng song song
Nếu một đường thẳng cắt hai đường thẳng song song thì:
a) Hai góc sole trong bằng nhau.
b) Hai góc đồng vị bù nhau.
c) Hai góc trong cùng phía bù nhau.
4.
1. Định lí Pytago Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
2.
1. Định lí Pytago

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
∆ABC vuông tại A.
=> BC2=AB2+AC2
2. Định lí Pytago đảo.
Nếu một tam giác có bình phương của một cạnh bẳng tổng bình phương các cạnh còn lại thì tam giác đó là tam giác vuông.
∆ABC :BC2=AB2+AC2
=> ˆBACBAC^= 902.

1.
Đường trung trực của đoạn thẳng là đường vuông góc với đường thẳng đó tại trung điểm.
2.
Những điểm thuộc đường trung trực của 1 đoạn thẳng thì luôn cách đều 2 mút của đoạn thẳng đó.
3.
Những điểm cách đều 2 mút của 1 đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng ấy.
1.
Đường trung trực của đoạn thẳng là đường vuông góc với đường thẳng đó tại trung điểm.
2.
Những điểm thuộc đường trung trực của 1 đoạn thẳng thì luôn cách đều 2 mút của đoạn thẳng đó.
3.
Những điểm cách đều 2 mút của 1 đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng ấy.

Đường trung trực của đoạn thẳng là 1 đường thẳng vuông góc với đoạn thẳng và đi qua trung điểm của đoạn thẳng đó. Tính chất của đường trung trực của đoạn thẳng: Điểm nằm cách đều hai mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng

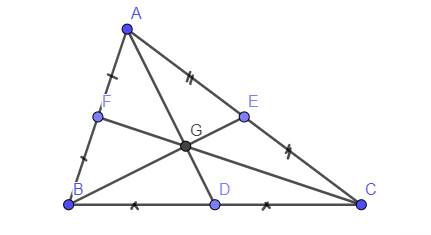
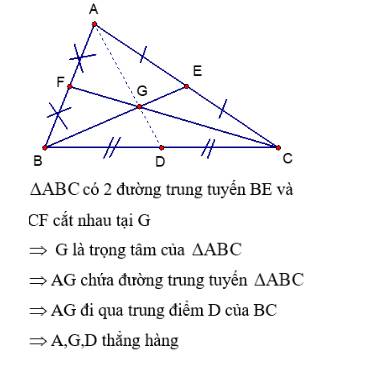
`+,` Có `D` là trung điểm của `BC(GT)`
`=>AD` là trung tuyến của `Delta ABC`
`+,` Có `BE` là trung tuyến của `Delta ABC`
`CF` là trung tuyến của `Delta ABC`
mà `BE` cắt `CF` tại `G`
nên `G` là trọng tâm của `Delta ABC`
+, Có `AD` là trung tuyến của `Delta ABC(cmt)`
mà `G` là trọng tâm của `Delta ABC`
nên `G in AD`
`=>A;D;G` thẳng hàng ( đpcm )
Đường cao của tam giác là đoạn vuông góc kẻ từ một đỉnh đến cạnh đối diện. Cạnh đối diện này được gọi là đáy ứng với đường cao. Độ dài của đường cao là khoảng cách giữa đỉnh và đáy.
Trong hình học phẳng, đường trung trực của một đoạn thẳng là đường vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó.Trong đường tròn, giao 2 tiếp tuyến thì điểm đó đến tâm là đường trung trực.
đường trung tuyến là một đường thẳng nối từ đỉnh của một tam giác tới trung điểm của cạnh tam giác đối diện.
Đường cao của tam giác là đoạn vuông góc kẻ từ một đỉnh đến cạnh đối diện
đường trung trực của một đoạn thẳng là đường vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó
trung tuyến của một tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện