Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số cần tìm là x.
+ Một nửa của x trừ đi một nửa đơn vị rồi nhân với một nửa của x là:
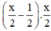
Theo bài ra ta có phương trình:
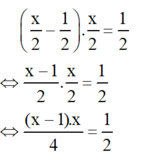
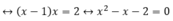
Có a = 1; b = -1; c = -2
⇒ a – b + c = 1 – (-1) – 2 = 0
⇒ Phương trình có hai nghiệm x1 = -1; x2 = 2.
Vậy số cần tìm là -1 hoặc 2.
Kiến thức áp dụng

Gọi số phải tìm là x.
một nửa của nó trừ đi một nửa đơn vị là: -
Theo đầu bài ta có phương trình: =
hay x2 – x – 2 = 0, có a – b + c = 1 – (-1) – 2 = 0 nên: x1 = -1, x2 = 2
Trả lời: Số phải tìm bằng -1 hoặc 2.
Gọi số phải tìm là x.
một nửa của nó trừ đi một nửa đơn vị là: -
Theo đầu bài ta có phương trình: =
hay x2 – x – 2 = 0, có a – b + c = 1 – (-1) – 2 = 0 nên: x1 = -1, x2 = 2
Trả lời: Số phải tìm bằng -1 hoặc 2.

Gọi tử là: x
mẫu là: y\(\left(y\ne0\right)\)
\(\Rightarrow x+y=32\left(1\right)\)
Vì khi tăng mẫu thêm 10 đơn vị và giảm tử đi 1 nửa thì được phân số mới bằng \(\frac{2}{17}\)
\(\Rightarrow\frac{x.0,5}{y+10}=\frac{2}{17}\Leftrightarrow8,5x-2y=20\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\hept{\begin{cases}x+y=32\\8,5x-2y=20\end{cases}\Leftrightarrow\hept{\begin{cases}x=8\\y=24\end{cases}}}\)
\(\Rightarrow\)Phân số cằn tìm là: \(\frac{8}{24}=\frac{1}{3}\)

Câu 2:
Gọi số phải tìm là ab
Vì tổng các chữ số của số cần tìm là 9 nên a+b=9(1)
Vì khi thêm vào số đó 63 đơn vị thì số thu được cũng viết bằng hai chữ số đó nhưng theo thứ tự ngược lại nên \(10a+b+63=10b+a\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}a+b=9\\10a+b+63=10b+a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=9-b\\10a+b+63-10b-a=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=9-b\\9a-9b=-63\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=9-b\\a-b=-7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=9-b\\9-b-b=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=9-b\\-2b=-16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=9-8=1\\b=8\end{matrix}\right.\)
Vậy: Số cần tìm là 18

Gọi chữ số hàng chục của số cần tìm là a; chữ số hàng đơn vị của số cần tìm là b (a, b \(\in\) N; 0 < a,b \(\le\) 9)
Số cần tìm là \(\overline{ab}=10a+b\)
Vì tổng bình phương của hai chữ số của nó bằng 89 nên ta có pt:
a2 + b2 = 89 (1)
Số sau khi đổi chỗ hai chữ số của số cần tìm là: \(\overline{ba}=10b+a\)
Vì nếu đổi chỗ hai chữ số của nó thì được một số nhỏ hơn số ban đầu là 27 đơn vị nên ta có pt:
\(\left(10a+b\right)-\left(10b+a\right)=27\)
\(\Leftrightarrow\) 9a - 9b = 27
\(\Leftrightarrow\) a - b = 3 (2)
Từ (1) và (2) ta có hpt:
\(\left\{{}\begin{matrix}a^2+b^2=89\\a-b=3\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}a^2+b^2=89\\a=3+b\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}\left(3+b\right)^2+b^2=89\\a=3+b\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}9+6b+2b^2=89\\a=3+b\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}b\left(3+b\right)=40\\a=3+b\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}a=8\\b=5\end{matrix}\right.\) (TM)
Vậy số cần tìm là 85
Chúc bn học tốt!
Gọi số cần tìm có dạng là \(ab\)(có dấu gạch ngang trên đầu)(Điều kiện: \(\left\{{}\begin{matrix}a,b\in N\\0< a< 10\\0\le a< 10\end{matrix}\right.\))
Vì tổng bình phương hai chữ số bằng 89 nên ta có phương trình:
\(a^2+b^2=89\)(1)
Vì khi đổi chỗ hai chữ số của nó thì được một số nhỏ hơn số ban đầu 27 đơn vị nên ta có phương trình:
\(10b+a+27=10a+b\)
\(\Leftrightarrow10b+a-10a-b=-27\)
\(\Leftrightarrow-9a+9b=-27\)
\(\Leftrightarrow-9\left(a-b\right)=-9\cdot3\)
\(\Leftrightarrow a-b=3\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}a^2+b^2=89\\a-b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(b+3\right)^2+b^2=89\\a=3+b\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b^2+6b+9+b^2=89\\a=3+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2b^2+6b-80=0\\a=b+3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b^2+3b-40=0\\a=b+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b^2+8b-5b-40=0\\a=b+3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b\left(b+8\right)-5\left(b+8\right)=0\\a=b+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(b+8\right)\left(b-5\right)=0\\a=b+3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}b+8=0\\b-5=0\end{matrix}\right.\\a=b+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}b=-8\left(loại\right)\\b=5\left(nhận\right)\end{matrix}\right.\\a=b+3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=5+3\\b=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=8\left(nhận\right)\\b=5\left(nhận\right)\end{matrix}\right.\)
Vậy: Số cần tìm là 85

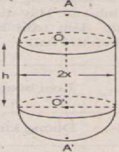
Ta có: AA’ = AO + OO’ + O’A’
hay 2a = x + h + x
hay 2x + h = 2a.
Gọi số cần tìm là x.
+ Một nửa của x trừ đi một nửa đơn vị rồi nhân với một nửa của x là:
Theo bài ra ta có phương trình:
Có a = 1; b = -1; c = -2
⇒ a – b + c = 1 – (-1) – 2 = 0
⇒ Phương trình có hai nghiệm x 1 = - 1 ; x 2 = 2 .
Vậy số cần tìm là -1 hoặc 2.
Kiến thức áp dụng
Để giải bài toán bằng cách lập phương trình ta làm theo các bước:
Bước 1: Lập phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn tất cả các đại lượng khác qua ẩn vừa chọn.
+ Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Bước 3: Đối chiếu điều kiện rồi kết luận.