Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x+3y\(\ge\)1=>x\(\ge\)1-3y
Suy ra: A\(\ge\)(1-3y)2+y2=1-6y+9y2+y2=10y2-6y+1=\(10.\left(y^2-\frac{3}{5}y+\frac{1}{10}\right)\)
\(=10.\left(y^2-2.y.\frac{3}{10}+\frac{9}{100}+\frac{1}{100}\right)=10.\left(x-\frac{3}{10}\right)^2+\frac{1}{10}\ge\frac{1}{10}=0,1\)
Vậy GTNN của A là 0,1 tại x=0,3

Đáp án C
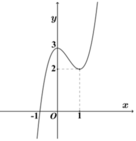
Vẽ đồ thị hàm số y = x 3 − 3 x 2 + 1

Để phương trình (1) có ba nghiệm phân biệt thỏa mãn x 1 < 1 < x 2 < x 3 thì đường thẳng y=m cắt đồ thị hàm số y = x 3 − 3 x 2 + 1 tại ba điểm phân biệt thỏa mãn x 1 < 1 < x 2 < x 3 ⇔ − 3 < m < − 1.

Đáp án B
Phương pháp: Đặt t = 2 x
Cách giải: Đặt t = 2 x ta có:
![]()
Khi đó phương trình trở thành
![]()
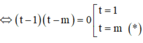
![]()
![]()
Để phương trình ban đầu có 3 nghiệm phân biệt ![]() có nghiệm
có nghiệm ![]()

ĐK: x ≥ 0
pt <=> 4x - 4√x +1 + x - 2√x .y + y^2 = 0
<=> (2√x -1)² + (√x -y)² = 0
(a² + b² = 0 <=> a và b bằng 0)
<=> hệ 2√x -1 = 0, √x -y = 0
<=> x = 1/4, y =1/2 (thỏa mãn)
KL: x=1/4, y = 1/2

Đáp án D
Phương trình có nghiệm ⇔ m 2 + 3 2 ≥ 5 2 ⇔ m 2 ≥ 16 ⇔ m ≤ − 4 m ≥ 4

Chọn C.
Đặt 2 log 3 x = t > 0
phương trình trở thành t 3 - 3 t = m
Bằng cách lập bảng biên thiên của hàm f t = t 3 - 3 t trên khoảng 0 ; + ∞ chúng ta dễ dàng thấy rằng phương trình có nhiều hơn một nghiệm (chính xác hơn là có hai nghiệm) khi và chỉ khi

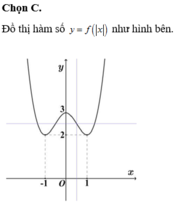
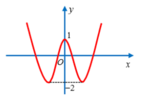
Đồ thị hàm số có điểm uốn là trung điểm của 2 đường cực trị I 1 2 ; 5 2
Số nghiệm của phương trình f(|x|)=m là số giao điểm của đồ thị hàm số y=f(|x|) và đường thẳng y=m. Để phương trình có 4 nghiệm thỏa mãn điều kiện đề bài thì 5 2 ≤ m < 3