Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp:
Phương trình bậc nhất đối với sin và cosasinx + bcosx = c vô nghiệm ![]()
Cách giải: Phương trình sinx + (m+1)cosx = 2 vô nghiệm
![]()
![]()

Đáp án A
Phương pháp: Chia cả 2 vế cho 3x, đặt  , tìm điều kiện của t.
, tìm điều kiện của t.
Đưa về bất phương trình dạng ![]()
Cách giải :
![]()

Ta có 

Đặt  , khi đó phương trình trở thành
, khi đó phương trình trở thành
![]()

![]()
![]()
![]()
![]()
Ta có: 



Vậy 

Đáp án A
Phương pháp: Đặt t = 4 x
Cách giải:
Đặt t = 4 x (t>0), khi đó phương trình trở thành:
![]()
![]()
Với t = 3 2 => Phương trình vô nghiệm
Với
t
≠
3
2
(t>0) phương trình trở thành 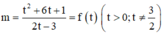
Để phương trình ban đầu có nghiệm 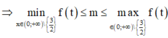
Xét hàm số 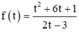 ta có:
ta có:
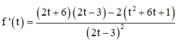
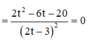
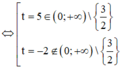
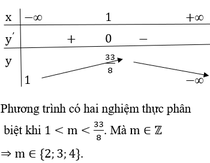
Lập BBT ta được :
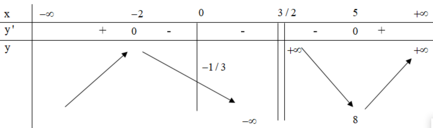
Để phương trình có nghiệm dương thì 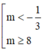

Đáp án C
PT ⇔ m x 2 + 2 x 3 − 2 x 2 + 2 x + 2 = 0
→ t = x 2 + 2 x m t 3 − 2 t + 2 = 0 1 .
Ta có: f x = x 2 + 2 x , x ≤ − 3 ⇒ f x ≥ 3 ⇒ t ∈ 3 ; + ∞
1 ⇔ m = 2 t 2 − 2 t 3 = f t với t ∈ 3 ; + ∞ .
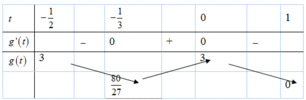
Ta có: f ' t = − 4 t 3 + 6 t 4 ⇒ f ' t = 0 ⇔ t = 3 2 ⇒ f t
nghịch biến trên 3 ; + ∞ ⇒ f 3 ; + ∞ t ≤ f 3 = − 2 27
Suy ra m ≤ − 2 27 ⇒ Có vô số giá trị của m.

Đáp án D
Ta có: 4 x − m .2 x + 1 + 2 m = 0 ⇔ 2 x 2 − 2 m .2 x + 2 m = 0
Giả thiết ⇔ Δ ' = m 2 − 2 m > 0 S = 2 m > 0 P = 2 m > 0 ⇔ m > 2
Khi đó: 2 x 1 + 2 x 2 = 2 m 2 x 1 .2 x 2 = 2 m ⇔ 2 x 1 + x 2 = 2 m ⇔ m = 4





Chọn C.
Đặt 2 log 3 x = t > 0
phương trình trở thành t 3 - 3 t = m
Bằng cách lập bảng biên thiên của hàm f t = t 3 - 3 t trên khoảng 0 ; + ∞ chúng ta dễ dàng thấy rằng phương trình có nhiều hơn một nghiệm (chính xác hơn là có hai nghiệm) khi và chỉ khi