Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt t = t ( x ) = 2 x + 2 - x với x ∈ [ - 1 ; 2 ]
Hàm t=t(x) liên tục trên [-1;2] và
t ' ( x ) = 2 x ln 2 - 2 - x ln 2 , t ' ( x ) = 0 ⇔ x = 0
Bảng biến thiên

Vậy x ∈ [ - 1 ; 2 ] ⇒ t ∈ 2 ; 17 4
Với mỗi t ∈ ( 2 ; 5 2 ] có 2 giá trị của x thỏa mãn t = 2 x + 2 - x
Với mỗi t ∈ 2 ∪ 5 2 ; 17 4 có duy nhất 1 giá trị x thỏa mãn.
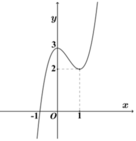
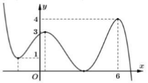
Xét phương trình f(t)=m với t ∈ 2 ; 17 4
Từ đồ thị, phương trình f ( 2 x + 2 - x ) = m có số nghiệm nhiều nhất khi và chỉ khi phương trình f(t)=m có 2 nghiệm t 1 , t 2 , trong đó có t 1 ∈ ( 2 ; 5 2 ] , t 2 ∈ ( 5 2 ; 17 4 ]
Khi đó, phương trình có nhiều nhất 3 nghiệm phân biệt thuộc đoạn [-1;2]
Chọn đáp án B.

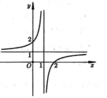
Chọn D.
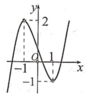
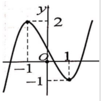
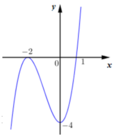
Để phương trình f(x)=m+2 có 4 nghiệm phân biệt thì đường thẳng y=m+2 phải cắt đồ thị hàm số y=f(x) tại 4 điểm phân biệt.
Dựa vào đồ thị ta được -4<m+2<-3 => -6<m<-5

Đáp án D
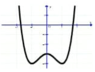
Hàm số y = f ( x ) đạt cực tiểu tại x 0 = 0
Hàm số y = f ( x ) có ba điểm cực trị.
Phương trình f ( x ) = 0 có 4 nghiệm phân biệt
Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]









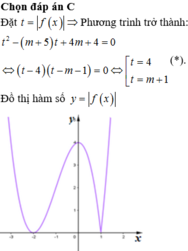


Đồ thị hàm số có điểm uốn là trung điểm của 2 đường cực trị I 1 2 ; 5 2
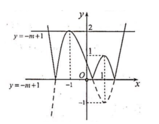
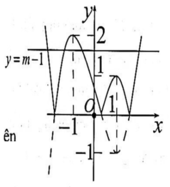
Số nghiệm của phương trình f(|x|)=m là số giao điểm của đồ thị hàm số y=f(|x|) và đường thẳng y=m. Để phương trình có 4 nghiệm thỏa mãn điều kiện đề bài thì 5 2 ≤ m < 3