Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

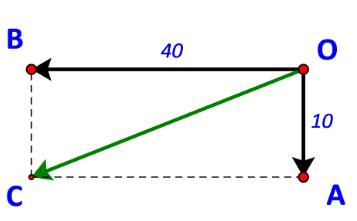
Gọi O là vị trí của ca nô.
Vẽ \(\overrightarrow {OA} \) là vận tốc dòng nước (chảy từ phía bắc xuống phía nam),
\(\overrightarrow {OB} \) là vận tốc riêng của ca nô (chuyển động từ phía đông sang phía tây)
Khi đó vecto vận tốc của ca nô so với bờ sông là vecto \(\overrightarrow {OA} + \overrightarrow {OB} \)
Gọi C là đỉnh thứ tư của hình bình hành OACB, ta có: \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \)
Xét tam giác OBC vuông tại B ta có:
BC = 40; BC = OA = 10.
\( \Rightarrow OC = \sqrt {O{B^2} + B{C^2}} = 10\sqrt {17} \)
Vậy vận tốc của ca nô so với bờ sông là \(10\sqrt {17} \) km/h.

Người đó chuyển động theo quỹ đạo đường tròn nên để xác định phương trình quỹ đạo chuyển động của người đó ta cần phải lập phương trình đường tròn.


Vẽ vecto \(\overrightarrow {AB} \) là vecto vận tốc của máy bay, \(\overrightarrow {AD} \) là vecto vận tốc của gió.
Khi đó vecto vận tốc mới của máy bay là \(\overrightarrow {AB} + \overrightarrow {AD} \)
Dựng hình bình hành ABCD. Ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\)
Mà AB = 700, BC = AD = 40, \(\widehat B = {135^o}\)
\(\begin{array}{l} \Rightarrow A{C^2} = {700^2} + {40^2} - 2.700.40.\cos {135^o} \approx 531197,98\\ \Leftrightarrow AC \approx 728,83\end{array}\)
Vậy tốc độ mới của máy bay là 728,83 km/h.

a) Ta có: Vận tốc đầu ở đỉnh dốc = 0 ( v0= 0) quả cầu chuyển động nhanh dần đều
S = 0 + (1/2).a.t²
=> a = 2.S/t²
= 2.100/10²
= 2 m/s²
ta có:
- Quả cầu nằm ngang trên mặt phẳng và chuyển động chậm dần với gia tốc a'
- Tốc độ đầu v là tốc độ tại chân dốc, tốc độ cuối = 0
v = 0 + a.t
= 0 + 2.10
= 20 (m/s)
Ta lại có: 0² - v² = 2.a'S
=> a' = -v²/2S
= - 20²/2.50
= - 4 (m/s²) ( vật chuyển động chậm dần đều )
b) Thời gian mà vật chuyển động trên mặt phẳng ngang t' là:
0 = v - a't'
=> t' = v/a' = 20/4 = 5 (s)
Thời gian quả cầu chuyển động trong cả quá trình là:
t + t' = 10 + 5 = 15 (s)
a)* Từ đỉnh dốc vận tốc đầu = 0, quả cầu chuyển động nhanh dần
S = 0 + (1/2)at²
=> a = 2S/t² = 2*100/10² = 2 m/s²
*Trên mặt phẳng ngang quả cầu chuyển động chậm dần với gia tốc a', tốc độ đầu v là tốc độ tại chân dốc, tốc độ cuối = 0
v = 0+at = 0 + 2.10 = 20 m/s
Có: 0² - v² = 2.a'S
=> a' = -v²/2S = -20²/2.50 = -4 (m/s²) (dấu - chứng tỏ vật cđộng chậm dần)
b) thời gian chuyển động trên mặt phẳng ngang: t'
0 = v - a't' => t' = v/a' = 20/4 = 5s
thời gian của cả quá trình chuyển động: t + t' = 10 + 5 = 15s
Chúc bạn học tốt !!!

a) Vật thể đi qua điểm \(A\left( {2;1} \right)\) và đi theo hướng vectơ \(\overrightarrow v \left( {3;4} \right)\).
b) Sau thời gian t thì vectơ vận tốc của vật thể là: \(t\overrightarrow v = \left( {3t;4t} \right)\).
Vậy tọa độ của vật thể sau thời gian t là: \(\overrightarrow {OA} + t\overrightarrow v = \left( {2 + 3t;1 + 4t} \right)\).

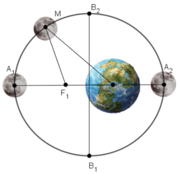
Theo đề bài có:
Độ dài trục lớn của elip bằng 769266km ⇒ A1A2 = 2a = 769266 ⇒ a = 384633
Độ dài trục nhỏ của elip bằng 768106km ⇒ B1B2 = 2b = 768106 ⇒ b = 384053
⇒ c2 = a2 – b2 = 445837880 ⇒ c ≈ 21115
⇒ F1F2 = 2c = 42230
⇒ A1F1 = A2F2 = (A1A2 – F1F2)/2 = 363518
+ Trái Đất gần Mặt Trăng nhất khi Mặt Trăng ở điểm A2
⇒ khoảng cách ngắn nhất giữa Trái Đất và Mặt Trăng bằng A2F2 = 363518 km
+ Trái Đất xa Mặt Trăng nhất khi Mặt Trăng ở điểm A1
⇒ khoảng cách xa nhất giữa Trái Đất và Mặt Trăng bằng:
A1F2 = A1F1 + F1F2 = 405748 km.