Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi BM=x km (0<x<7)
=> MC=7-x (km)
Ta có: \(AM = \sqrt {A{B^2} + B{M^2}} \)\( = \sqrt {16 + {x^2}} \left( {km} \right)\)
Thời gian từ A đến M là: \(\frac{{\sqrt {16 + {x^2}} }}{3}\left( h \right)\)
Thời gian từ M đến C là: \(\frac{{7 - x}}{5}\left( h \right)\)
Tổng thời gian từ A đến C là 148 phút nên ta có:
\(\begin{array}{l}\frac{{\sqrt {16 + {x^2}} }}{3} + \frac{{7 - x}}{5} = \frac{{148}}{{60}}\\ \Leftrightarrow \frac{{\sqrt {16 + {x^2}} }}{3} + \frac{{7 - x}}{5} = \frac{{37}}{{15}}\\ \Leftrightarrow \frac{{5\sqrt {16 + {x^2}} }}{{15}} + \frac{{3.\left( {7 - x} \right)}}{{15}} = \frac{{37}}{{15}}\\ \Leftrightarrow 5\sqrt {16 + {x^2}} + 3.\left( {7 - x} \right) = 37\\ \Leftrightarrow 5\sqrt {16 + {x^2}} = 16 + 3x\\ \Leftrightarrow 25.\left( {16 + {x^2}} \right) = 9{x^2} + 96x + 256\\ \Leftrightarrow 16{x^2} - 96x + 144 = 0\\ \Leftrightarrow x = 3\left( {tm} \right)\end{array}\)
Vậy khoảng cách từ vị trí B đến M là 3 km.

Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{ABC}+59^0+82^0=180^0\)
=>\(\widehat{ABC}=39^0\)
Xét ΔABC có \(\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
=>\(\dfrac{25}{sin39}=\dfrac{AB}{sin82}\)
=>\(AB=25\cdot\dfrac{sin82}{sin39}\simeq39,34\left(m\right)\)

Đổi: 1 km = 1000 m. Do đó AC = 1000 m.
Áp dụng định lí cosin trong tam giác ABC ta có:
\(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C\)
\(\begin{array}{l} \Rightarrow A{B^2} = {1000^2} + {800^2} - 2.1000.800.\cos {105^o}\\ \Rightarrow A{B^2} \approx 2054110,5\\ \Rightarrow AB \approx 1433,2\end{array}\)
Vậy khoảng cách AB là 1433,2 m.

Đặt x=B'C(km), 0<=x<=9
=>\(BC=\sqrt{x^2+36};AC=9-x\)
Chi phí xây dựng dường ống là:
\(C\left(x\right)=130000\sqrt{x^2+36}+50000\left(9-x\right)\left(USD\right)\)
Hàm C(x) xác định và liên tục trên [0;9] và \(C'\left(x\right)=10000\left(\dfrac{13x}{\sqrt{x^2+36}}-5\right)\)
C'(x)=0
=>13x=5 căn x^2+36
=>x=5/2

Giải tam giác là việc đi tìm một số yếu tố của tam giác khi đã biết các yếu tố khác của tam giác đó.
Trong trường hợp này, giải tam giác ABC được hiểu là tìm cạnh AC khi biết cạnh AB, góc A và góc B.
Áp dụng định lí sin ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
Mà \(AB=d, \hat {B} =\beta; \hat {C} =180^o-\alpha -\beta \)
\(\Rightarrow AC = \sin \beta \frac{d}{{\sin \left( {{{180}^o} - \alpha - \beta } \right)}}\)

Tham khảo:
a)
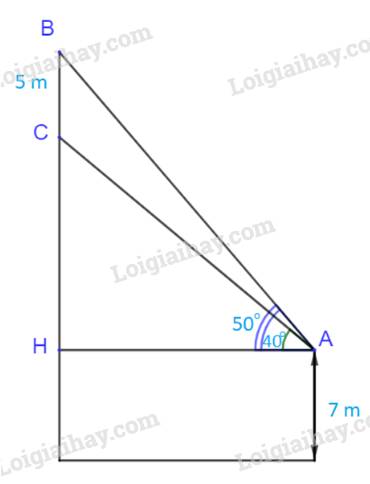
Gọi H là hình chiếu của A lên đường thẳng BC.
Ta có: \(\widehat {HAB} = {50^o}\); \(\widehat {HAC} = {40^o}\)
\( \Rightarrow \widehat {BAC} = {50^o} - {40^o} = {10^o}\) (1)
Xét tam giác ABH, vuông tại H ta có:
\(\widehat H = {90^o};\;\widehat {BAH} = {50^o}.\)
\( \Rightarrow \widehat {HBA} = {180^o} - {90^o} - {50^o} = {40^o}\) hay \(\widehat {CBA} = {40^o}\). (2)
Từ (1) và (2), suy ra: \(\widehat {BCA} = {180^o} - {40^o} - {10^o} = {130^o}.\)
Vậy ba góc của tam giác ABC lần lượt là: \(\widehat A = {10^o};\;\widehat B = {40^o};\;\widehat C = {130^o}\).
b)
Áp dụng định lý sin cho tam giác ABC, ta được:
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\) \( \Rightarrow AB = \frac{{BC.\sin C}}{{\sin A}}\)
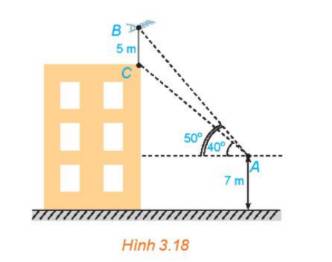
Mà: \(BC = 5\;(m);\;\;\widehat C = {130^o};\;\widehat A = {10^o}\)
\( \Rightarrow AB = \frac{{5.\sin {{130}^o}}}{{\sin {{10}^o}}} \approx 22\;(m)\)
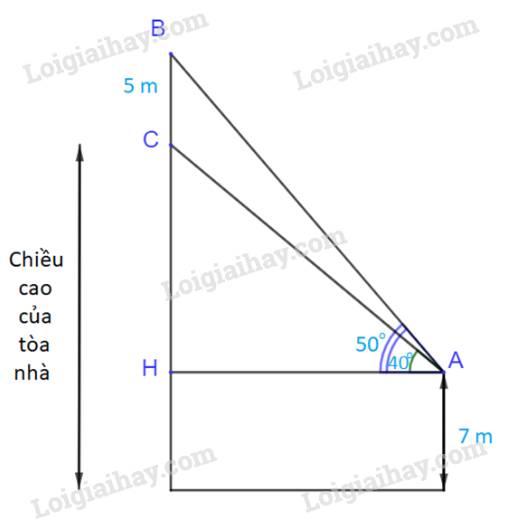
Xét tam giác ABH, vuông tại H ta có:
\(\sin \widehat {BAH} = \frac{{BH}}{{AB}}\)\( \Rightarrow BH = AB.\,\,\sin \widehat {BAH}\)
Mà: \(AB \approx 22\;(m);\;\;\widehat {BAH} = {50^o}\)
\( \Rightarrow BH \approx 22.\sin {50^o} \approx 16,85\;(m)\)
Vậy chiều cao của tòa nhà là: \(BH-{\rm{ }}BC + 7 = 16,85-5 + 7 = 18,85{\rm{ }}\left( m \right)\)

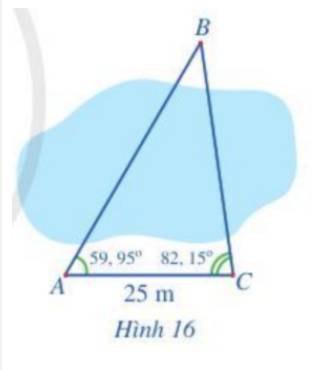
Xét tam giác ABC, ta có: \(\widehat {BAC} = 59,{95^o};\;\widehat {BCA} = 82,{15^o}.\)
\( \Rightarrow \widehat {ABC} = {180^o} - \left( {59,95 + 82,{{15}^o}} \right) = 37,{9^o}\)
Áp dụng định lí sin trong tam giác BAC ta có: \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow AB = \sin C.\frac{{AC}}{{\sin B}} = \sin 82,{15^o}.\frac{{25}}{{\sin {37,9^o}}} \approx 40\)
Vậy khoảng cách từ vị trí A đến vị trí B là 40 m.