
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

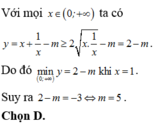

Chọn D
* Tập xác định ![]()
* Ta có 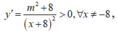
suy ra hàm số đã cho đồng biến trên đoạn [0;3].
Do đó 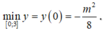
* Theo yêu cầu bài toán ta có: 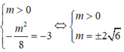
![]()

Đạo hàm f'(x) = m 2 - m + 1 ( x + 1 ) 2 > 0, ∀ x ∈ [ 0 ; 1 ]
Suy ra hàm số f(x) đồng biến trên [0; 1] nên min f(x) = f(0) = -m2+m
Theo bài ta có:
-m2+ m= -2 nên m= -1 hoặc m= 2.
Chọn D.

+ Đạo hàm f'(x) = 2 - m x 2 ( x + 1 ) x ( x + 1 )
f'(x) = 0 ⇒ x = 2 m ↔ x = m 2 4 ∈ [ 0 ; 4 ] , ∀ m > 1
+ Lập bảng biến thiên, ta kết luận được
m a x [ 0 ; 4 ] f ( x ) = f ( 4 m 2 ) = m 2 + 4
+ Vậy ta cần có m 2 + 4 < 3
↔ m < 5 → m > 1 m ∈ ( 1 ; 5 )
Chọn C.

Chọn B
Tập xác định D = ℝ \{1}
Ta có 
Do đó hàm số nghịch biến trên đoạn [2;3]
Suy ra ![]()
Vậy có 1 giá trị nguyên dương của m.

Chọn A.
TXĐ: D = R.
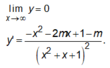
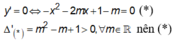 có 2 nghiệm phân biệt
có 2 nghiệm phân biệt ![]()
BBT:
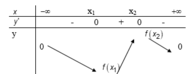
Vậy hàm số đạt giá trị lớn nhất là
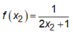
![]()
YCBT 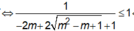
![]()
![]()
![]()
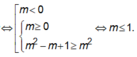

Chọn D
y = f(x) = - x 3 - 3 x 2 + m
Ta có:
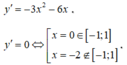
f(-1) = m - 2; f(0) = m; f(1) = m - 4;
Ta thấy ![]() Suy ra yêu cầu bài toán
Suy ra yêu cầu bài toán ![]()

3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)