Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

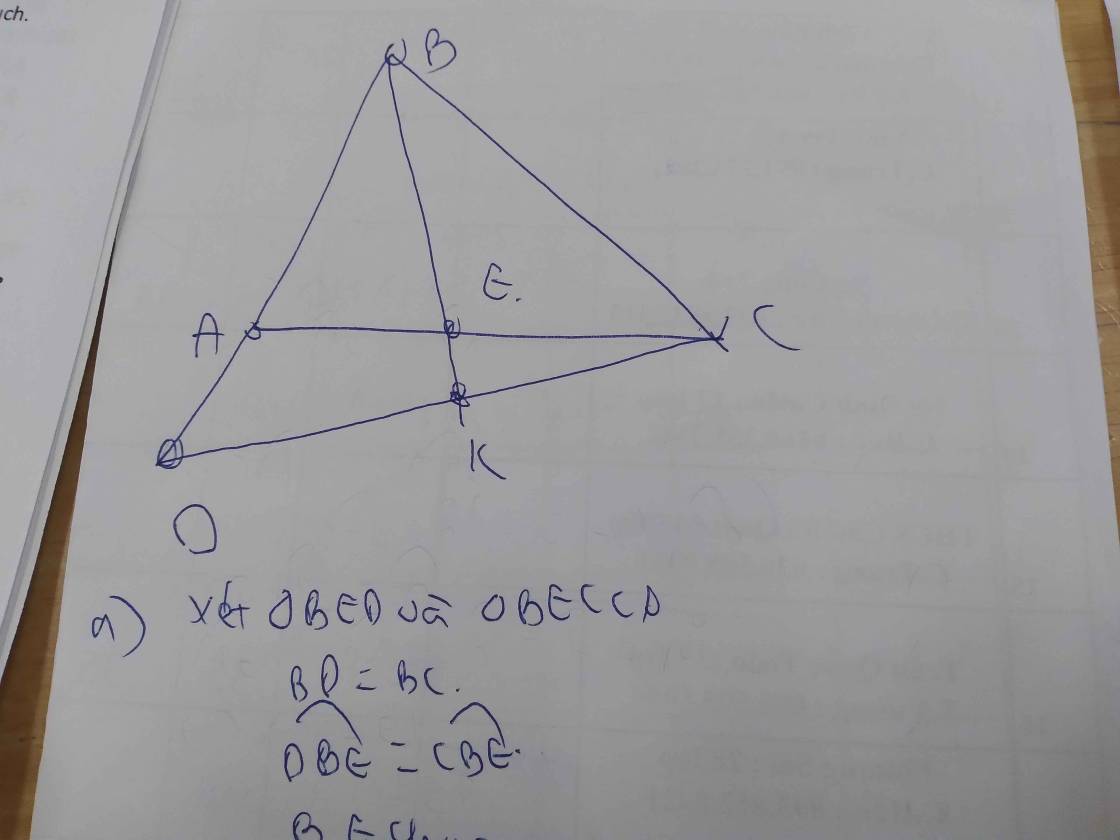
a: Xét ΔBDE và ΔBCE có
BD=BC
\(\widehat{DBE}=\widehat{CBE}\)
BE chung
Do đó: ΔBDE=ΔBCE
b: Ta có: ΔBDE=ΔBCE
=>ED=EC
=>E nằm trên đường trung trực của DC(1)
Ta có: BD=BC
=>B nằm trên đường trung trực của CD(2)
Ta có: KD=KC
=>K nằm trên đường trung trực của CD(3)
Từ (1),(2),(3) suy ra B,E,K thẳng hàng
=>B,E,K cùng nằm trên đường trung trực của DC
=>EK\(\perp\)DC
c: ΔAHD vuông tại H có \(\widehat{DAH}=45^0\)
nên ΔAHD vuông cân tại H
Xét ΔBDC có BD=BC
nên ΔBCD cân tại B
mà \(\widehat{BDC}=45^0\)
nên ΔBCD vuông cân tại B
=>\(\widehat{ABC}=90^0\)

a)Xét tam giác BED và tam giác BEC có:
BD=BC(gt)
Góc B1= góc B2 (Vì BK là tia phân giác của góc B)
BE chung
=> Tam giác BED= tam giác BEC(c.g.c)
b) Xét tam giác BKS và tam giác BKC có:
BK chung
Góc B1= góc B2 (Vì BK là tia phân giác của góc B)
DK=KC( vì K là trung điểm của DC)
=> Tam giác BKD= tam giác BKC(c.g.c)
=>BK vg góc với DC
hay EK vg góc với DC
c)VÌ EK vg góc với DC(cm b)
Mà BK vg góc với DC(cm b)
=> EK và BK cùng vg góc với DC
=> Ek trùng với BK
=>Ba điểm B,E,K thẳng hàng

a) Xét \(\Delta BED\) và \(\Delta BEC\) có:
\(BD=BC\) (giả thiết)
\(\widehat{DBE}=\widehat{CBE}\) (do \(BE\) là tia phân giác \(\widehat{B}\))
\(BE\) là cạnh chung
\(\Rightarrow\Delta BED=\Delta BEC\left(c.g.c\right)\)
b) Vì \(\Delta BED=\Delta BEC\left(cmt\right)\)
\(\Rightarrow ED=EC\) (\(2\) cạnh tương ứng)
\(\Rightarrow\Delta EDC\) cân tại \(E\)
Mà \(EK\) là đường trung tuyến \(\Delta EDC\)
\(\Rightarrow EK\) cũng là đường trung trực \(\Delta EDC\)
\(\Rightarrow EK\perp DC\)
c) Giả sử \(\Delta ABC\) vuông tại \(B\)
Ta có: \(\Delta DBC\) vuông cân tại \(B\)
\(\Rightarrow\widehat{ADC}=\widehat{BCD}=45^o\)
Xét \(\Delta ADH\left(\widehat{H}=90^o\right)\) có:
\(\widehat{ADH}+\widehat{DAH}=90^o\) (\(2\) góc phụ nhau)
\(\Rightarrow\widehat{DAH}=90^o-45^o=45^o\)
d) Ta có: \(BC=BD\) (giả thiết)
\(\Rightarrow\Delta BCD\) cân tại \(B\)
Mà \(BE\) là đường phân giác \(\widehat{B}\) (giả thiết)
\(\Rightarrow BE\) cũng là đường cao \(\Delta BCD\)
\(\Rightarrow BE\perp DC\)
Lại có: \(EK\perp DC\left(cmt\right)\)
\(\Rightarrow B,K,E\) thẳng hàng

a) Xét ΔBED và ΔBEC có
BD=BC(gt)
\(\widehat{DBE}=\widehat{CBE}\)(BE là tia phân giác của \(\widehat{DBC}\))
BE chung
Do đó: ΔBED=ΔBEC(c-g-c)
Xét ΔBDI và ΔBCI có
BD=BC(gt)
\(\widehat{DBI}=\widehat{CBI}\)(BI là tia phân giác của \(\widehat{DBC}\))
BI chung
Do đó: ΔBDI=ΔBCI(c-g-c)
⇒ID=IC(hai cạnh tương ứng)
b) Sửa đề: Chứng minh AH//BI
Xét ΔBDC có BD=BC(gt)
nên ΔBDC cân tại B(Định nghĩa tam giác cân)
Ta có: ΔBDC cân tại B(cmt)
mà BI là đường phân giác ứng với cạnh đáy DC(gt)
nên BI là đường cao ứng với cạnh DC(Định lí tam giác cân)
⇒BI⊥DC
Ta có: AH⊥DC(gt)
BI⊥DC(cmt)
Do đó: AH//BI(Định lí 1 từ vuông góc tới song song)