Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Khi ω = ω1 thì 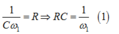
Khi ω = ω2 thì 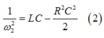
Khi ω = ω0 thì
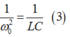
Thay (1) và (3) và (2) ta thu được 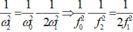

Ta có: cos φ = 2 m − 1 m = 1 3 ⇒ m ≈ 0 , 55
→ Với m = f C f L = f 0 f 0 + 5 6 = 0 , 55 → S H I F T + S O L V E f 0 = 15 Hz
Đáp án B

Đáp án A
f
L
thì
U
L
max;
f
L
1
và
f
L
2
thì
U
L
như nhau thì 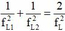
Tương tự với
U
C
, có ![]()
Để ý thấy, f thay đổi làm cho U L = U thì f L 1 = ∞; U C = U thì f C 1 = 0
Suy ra ![]()
![]()
Với các bài toán xảy ra công thức (1), ta đều có Z L , Z C đổi chỗ cho nhau trong 2 trường hợp tần số f L , f C . Đồng thời cosφ trong cả 2 trường hợp cũng bằng nhau.
Đặt 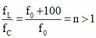 Có
Có ![]()
Có 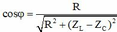
![]()
Mặt khác ![]()
![]()
Từ 2 pt trên, dễ dàng tìm được 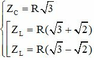
Vì n > 1 nên Z L > Z C => chọn
Từ đó tính được ![]()

Ta có ω 1 2 = 1 L C
Chuẩn hóa R = 1 Z L = x ⇒ Z C = x
Giả sử rằng tần số góc ω 2 = n ω 1 , khi đó ta có
U A M = U 1 2 + n x 2 1 2 + n x − x n 2 = U 1 + x 2 n 2 − 2 x 2 1 + n x 2
Để U A M không phụ thuộc vào R thì
x 2 n 2 − 2 x 2 = 0 ⇒ x = 0 n = 1 2 ⇒ f 2 = f 1 2
Đáp án D

- Trường hợp 1: Xét:
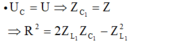
- Trường hợp 2: Xét:
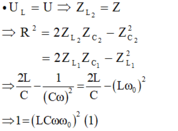
- Đồng thời:
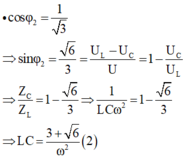
- Vì f = f0 + 75 (Hz) nên ω = ω0 + 150π
- Thay (2) vào (1) ta có:
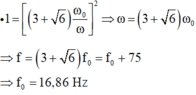

Đáp án A
+ f = 50 Hz: ![]()
+ f = 125 Hz: ![]()
Vì
Z
L
.
Z
C
= L/C luôn không đổi nên suy ra ![]()
Mặt khác ![]() (1)
(1)
+ f = f 0 : u R L sớm so với uC, suy ra φ R L = 45 0 => R = Z L 0 (2)
Từ (1) và (2) suy ra f 0 = 2 f 1 = 100 H z

Đáp án A
fL thì UL max; fL1 và fL2 thì UL như nhau thì 1 f L 1 2 + 1 f L 2 2 = 2 f L 2
Tương tự với UC, có f C 1 2 + f C 2 2 = 2 f C 2
Để ý thấy, f thay đổi làm cho UL = U thì fL1 = ∞; UC = U thì fC1 = 0.
Suy ra f L 2 = f 0 + 100 = f L 2 ; f C 2 = f 0 = f C 2 ⇒ f 0 ( f 0 + 100 ) = f L f C = f C H 2 (1)
Với các bài toán xảy ra công thức (1), ta đều có ZL và ZC đổi chỗ cho nhau trong 2 trường hợp tần số fL và fC. Đồng thời cosφ trong cả 2 trường hợp cũng bằng nhau.
Đặt f L f C = f 0 + 100 f 0 = n > 1 . Có Z C = Z L ' = n Z L ⇒ n = Z C Z L
Có c os φ = R R 2 + ( Z L − Z C ) 2 ⇒ ( Z L − Z C ) 2 = 2 R 2
Mặt khác U C = U ⇒ Z C = Z ⇔ Z C 2 = R 2 + ( Z L − Z C ) 2
Từ 2 pt trên, dễ dàng tìm được Z C = R 3 Z L = R ( 3 + 2 ) Z L = R ( 3 − 2 )
Vì n > 1 nên ZC > ZL => chọn Z L = R ( 3 − 2 ) ⇒ n = 3 + 6
Từ đó tính được f 0 = 22 , 475 ( H z )
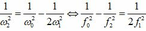
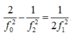
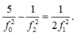
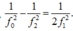
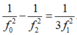
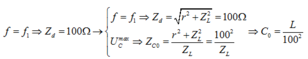
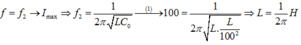
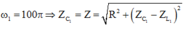
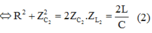
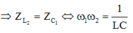
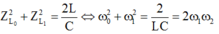
đáp án D mà