Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
BE/BC=BD/BA
nên ED//AC và ED=AC/2
=>ED//AF và ED=AF
=>ADEF là hình bình hành
mà góc FAD=90 độ
nên ADEF là hình chữ nhật
b: Xét tứ giác BMAE có
D là trung điểm chung của BA vàME
EA=EB
Do đó: BMAE là hình thoi
c: \(AC=\sqrt{5^2-3^2}=4\left(cm\right)\)
S=1/2*3*4=6(cm2)

Xét tam giác vuông ABC có:
\(AB^2+AC^2=BC^2\\ =>3^2+AC^2=5^2\\ =>AC^2=16\\ =>AC=4cm\)

a: Xet ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: ΔABC vuông tại A có AH vuông góc BC
nên AB^2=BH*BC
ΔABC vuông tại A có AH vuông góc BC
nên AH^2=HB*HC

Lời giải:
Tứ giác $AEDF$ có 3 góc vuông $\widehat{E}=\widehat{A}=\widehat{F}=90^0$ nên $AEDF$ là hình chữ nhật.

a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=5^2-3^2=16\)
=>\(AC=\sqrt{16}=4\left(cm\right)\)
Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)
=>\(\dfrac{AD}{3}=\dfrac{CD}{5}\)
mà AD+CD=AC=4
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{3}=\dfrac{CD}{5}=\dfrac{AD+CD}{3+5}=\dfrac{4}{8}=\dfrac{1}{2}\)
=>\(AD=\dfrac{3}{2}=1,5\left(cm\right)\)
b: Xét ΔCHD vuông tại H và ΔCAB vuông tại A có
\(\widehat{HCD}\) chung
Do đó: ΔCHD đồng dạng với ΔCAB
=>\(\dfrac{CH}{CA}=\dfrac{CD}{CB}\)
=>\(CH\cdot CB=CA\cdot CD\)
c: Ta có: AE\(\perp\)BC
DH\(\perp\)BC
Do đó: HD//AE
Xét ΔAEC có HD//AE
nên \(\dfrac{HC}{HE}=\dfrac{CD}{DA}\)
mà \(\dfrac{CD}{DA}=\dfrac{BC}{BA}\)
nên \(\dfrac{HC}{HE}=\dfrac{BC}{BA}\)
d: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔBAD=ΔBHD
=>BA=BH và DA=DH
Ta có: BA=BH
=>B nằm trên đường trung trực của AH(1)
Ta có: DA=DH
=>D nằm trên đường trung trực của AH(2)
Từ (1),(2) suy ra BD là đường trung trực của AH
=>BD\(\perp\)AH tại O và O là trung điểm của AH
=>OA=OH(3)
Xét ΔCMN có AO//MN
nên \(\dfrac{AO}{MN}=\dfrac{CO}{CM}\left(4\right)\)
Xét ΔCBM có OH//BM
nên \(\dfrac{OH}{BM}=\dfrac{CO}{CM}\left(5\right)\)
Từ (3),(4),(5) suy ra MN=BM
=>M là trung điểm của BN

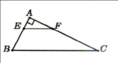
a) Xét ΔAMF có
AE là đường cao ứng với cạnh MF(\(AE\perp MF\))
AE là đường trung tuyến ứng với cạnh MF(E là trung điểm của MF)
Do đó: ΔAMF cân tại A(Định lí tam giác cân)
hay AM=AF(1)
Xét ΔCFM có
CE là đường cao ứng với cạnh MF(\(CE\perp MF\))
CE là đường trung tuyến ứng với cạnh MF(E là trung điểm của MF)
Do đó: ΔCFM cân tại C(Định lí tam giác cân)
hay CM=CF(2)
Vì ΔABC vuông tại A(gt) có AM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(AM=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(CM=BM=\dfrac{BC}{2}\)(M là trung điểm của BC)
nên AM=CM=BM(3)
Từ (1), (2) và (3) suy ra AM=AF=CF=CM=BM
Xét tứ giác AMCF có AM=CM=CF=FA(cmt)
nên AMCF là hình thoi(Dấu hiệu nhận biết hình thoi)
b)
Sửa đề: Tìm điều kiện của ΔABC để tứ giác AMCF là hình vuông
Hình thoi AMCF trở thành hình vuông khi \(\widehat{AMC}=90^0\)
hay \(AM\perp BC\)
Xét ΔABC có
AM là đường cao ứng với cạnh BC(\(AM\perp BC\))
AM là đường trung tuyến ứng với cạnh BC(M là trung điểm của BC)
Do đó: ΔABC cân tại A(Định lí tam giác cân)
hay AB=AC
Vậy: Khi ΔABC có thêm điều kiện AB=AC thì AMCF trở thành hình vuông
c)
Ta có: MD\(\perp\)AB(gt)
AC\(\perp\)AB(ΔABC vuông tại A)
Do đó: MD//AC(Định lí 1 từ vuông góc tới song song)
Xét ΔABC có
M là trung điểm của BC(gt)
MD//AC(cmt)
Do đó: D là trung điểm của AB(Định lí 1 đường trung bình của tam giác)
Xét ΔABC có
M là trung điểm của BC(gt)
D là trung điểm của AB(cmt)
Do đó: MD là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
nên \(MD=\dfrac{AC}{2}\)(Định lí 2 đường trung bình của tam giác)(1)
Ta có: \(ME\perp AC\)(gt)
\(AB\perp AC\)(ΔABC vuông tại A)
Do đó: ME//AB(Định lí 1 từ vuông góc tới song song)
Xét ΔABC có
M là trung điểm của BC(gt)
ME//AB(cmt)
Do đó: E là trung điểm của AC(Định lí 1 đường trung bình của tam giác)
nên \(CE=\dfrac{AC}{2}\)(2)
Từ (1) và (2) suy ra MD=CE
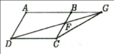
Xét tứ giác CMDE có
MD//CE(MD//AC)
MD=CE(cmt)
Do đó: CMDE là hình bình hành(Dấu hiệu nhận biết hình bình hành)
nên Hai đường chéo CD và EM cắt nhau tại trung điểm của mỗi đường(Định lí hình bình hành)
mà I là trung điểm của EM(gt)
nên I là trung điểm của CD(đpcm)

a: Ta có: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC^2=25+49=74\)
=>\(BC=\sqrt{74}\left(cm\right)\)
Xét ΔABC có AD là phân giác
nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)
=>\(\dfrac{DB}{5}=\dfrac{DC}{7}\)
mà \(DB+DC=BC=\sqrt{74}\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{5}=\dfrac{DC}{7}=\dfrac{DB+DC}{5+7}=\dfrac{\sqrt{74}}{12}\)
=>\(DB=\dfrac{\sqrt{74}}{12}\cdot5=\dfrac{5\sqrt{74}}{12}\left(cm\right);DC=\dfrac{7\sqrt{74}}{12}\left(cm\right)\)
b: Xét ΔCAB có ED//AB
nên \(\dfrac{CE}{CA}=\dfrac{CD}{CB}=\dfrac{ED}{AB}\)
=>\(\dfrac{CE}{7}=\dfrac{ED}{5}=\dfrac{7\sqrt{74}}{12}:\sqrt{74}=\dfrac{7}{12}\)
=>\(CE=\dfrac{7}{12}\cdot7=\dfrac{49}{12}\left(cm\right);ED=7\cdot\dfrac{5}{12}=\dfrac{35}{12}\left(cm\right)\)
c: Xét ΔABC vuông tại A và ΔEDC vuông tại E có
\(\widehat{ACB}\) chung
Do đó: ΔABC~ΔEDC
=>\(k=\dfrac{BC}{DC}=\sqrt{74}:\dfrac{7\sqrt{74}}{12}=\dfrac{12}{7}\)