K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
21 tháng 8 2023
\(2x+3x+5x+...+17x+19x\)
\(x.\left(2+3+5+...+17+19\right)=1+2+...+9\)
\(x.101=45\)
\(\Rightarrow x=45:101\)
\(\Rightarrow x=\dfrac{45}{101}\)
NT
(đề bài: tìm x biết)
1
15 tháng 12 2023
a: \(\left(x+10\right)\left(x-5\right)=0\)
=>\(\left[{}\begin{matrix}x+10=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-10\\x=5\end{matrix}\right.\)
b: \(\left(2x+10\right)\left(4+x\right)=0\)
=>\(\left[{}\begin{matrix}2x+10=0\\4+x=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-4\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=-5\end{matrix}\right.\)
c: \(\left(4x+20\right)\left(12x-24\right)=0\)
=>\(\left[{}\begin{matrix}4x+20=0\\12x-24=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x=-20\\12x=24\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-5\\x=2\end{matrix}\right.\)
d: \(\left(x-2024\right)\left(4x+4\right)=0\)
=>\(\left[{}\begin{matrix}x-2024=0\\4x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2024\\4x=-4\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-1\\x=2024\end{matrix}\right.\)
e: \(\left(2x-6\right)\left(7+x\right)=0\)
=>\(\left[{}\begin{matrix}2x-6=0\\x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\x=-7\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=3\\x=-7\end{matrix}\right.\)
g: (4x+8)(6-x)=0
=>\(\left[{}\begin{matrix}4x+8=0\\6-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x+2=0\\x=6\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-2\\x=6\end{matrix}\right.\)
h: (2x+2)(4x-8)=0
=>2(x+1)*4*(x-2)=0
=>(x+1)(x-2)=0
=>\(\left[{}\begin{matrix}x+1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
i: (2x-2024)(8x-16)=0
=>\(2\left(x-1012\right)\cdot8\cdot\left(x-2\right)=0\)
=>\(\left(x-1012\right)\left(x-2\right)=0\)
=>\(\left[{}\begin{matrix}x-1012=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1012\\x=2\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
27 tháng 4 2023
Lời giải:
$\frac{x+1}{3}=\frac{25}{-5}=-5$
$x+1=3(-5)=-15$
$x=-15-1=-16$
MS
15 tháng 12 2023
Ta có: \(ab+12=a+b\)
\(\Leftrightarrow a\left(b-1\right)-\left(b-1\right)+11=0\)
\(\Leftrightarrow\left(b-1\right)\left(a-1\right)=-11\)
Vì \(a,b\in Z\) nên \(\left(a-1\right),\left(b-1\right)\inƯ\left(-11\right)=\left\{\pm1,\pm11\right\}\)
Ta có bảng sau:
| a-1 | 1 | -1 | 11 | -11 |
| b-1 | -11 | 11 | -1 | 1 |
| a | 2 | 0 | 12 | -10 |
| b | -10 | 12 | 0 | 2 |
Vậy \(\left(a,b\right)\in\left\{\left(2;-10\right),\left(0;12\right),\left(12;0\right),\left(-10;2\right)\right\}\)
NG
2
NN
24 tháng 1
4y + 2549 = x(x + 1)
Vì x(x + 1) là tích của 2 số tự nhiên liên tiếp nên x(x + 1) chẵn
=> 4y + 2549 chẵn
=> 4y lẻ
=> y = 0
=> 40 + 2550 = x(x + 1)
=> 2550 = x(x + 1) = 50 . 51
=> x = 50
D
16 tháng 12 2022
Vì \(x^2 \ge 0\) với mọi `x`
\(=>x^{2}+2021 \ge 2021\) với mọi `x`
Hay \(A \ge 2021\) với mọi `x`
Dấu "`=`" xảy ra `<=>x=0`
NL
4
15 tháng 5 2017
xy + x - y = 6
\(\Rightarrow x\left(y+1\right)-y-1=5\)
\(\Rightarrow x\left(y+1\right)-\left(y+1\right)=5\)
\(\Rightarrow\left(x-1\right)\left(y+1\right)=5\)
Ta có bảng sau:
| x - 1 | 1 | -1 | 5 | -5 |
| y + 1 | 5 | -5 | 1 | -1 |
| z | 2 | 0 | 6 | -4 |
| y | 4 | -6 | 0 | -2 |
Vậy...
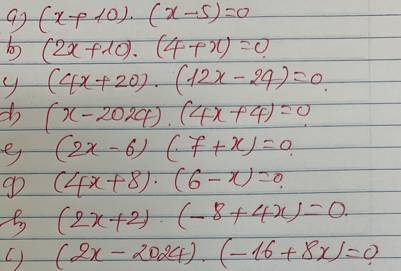
đề kiểu gì dzậy
ab có thể bằng bất kì số nào nhưng a và b không giống nhau
Hok tốt
# MissyGirl #