K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
XO
10 tháng 7 2023
ĐKXĐ : \(x^4+\left(\sqrt{3}-\sqrt{2}\right).x^2-\sqrt{6}\ne0\)
\(\Leftrightarrow x\ne\sqrt[4]{2}\)
\(P=\dfrac{x^2-\sqrt{2}}{x^4+\left(\sqrt{3}-\sqrt{2}\right).x^2-\sqrt{6}}\)
\(=\dfrac{x^2-\sqrt{2}}{\left(x^4-\sqrt{2}x^2\right)+\sqrt{3}\left(x^2-\sqrt{2}\right)}\)
\(=\dfrac{x^2-\sqrt{2}}{\left(x^2+\sqrt{3}\right)\left(x^2-\sqrt{2}\right)}=\dfrac{1}{x^2+\sqrt{3}}\)
11 tháng 7 2023
4:
a: cos^2a=1-(1/2)^2=1-1/4=3/4
=>\(cosa=\dfrac{\sqrt{3}}{2}\)
\(tana=\dfrac{1}{2}:\dfrac{\sqrt{3}}{2}=\dfrac{1}{\sqrt{3}}\)
\(cota=1:\dfrac{1}{\sqrt{3}}=\sqrt{3}\)
b: sin^2a=1-(3/4)^2=1-9/16=7/16
=>\(sina=\dfrac{\sqrt{7}}{4}\)
\(tana=\dfrac{\sqrt{7}}{4}:\dfrac{3}{4}=\dfrac{\sqrt{7}}{3}\)
\(cota=1:\dfrac{\sqrt{7}}{3}=\dfrac{3}{\sqrt{7}}\)
12 tháng 1 2023
a: Xét tứ giác ABOC có
góc OBA+góc OCA=180 độ
nên OBAC là tứ giác nội tiếp
Tâm là trung điểm của OA
R=OA/2
b: Xét ΔABD và ΔAEB có
góc ABD=góc AEB
góc BAE chung
Do đó: ΔABD đồng dạng với ΔAEB
=>AB/AE=AD/AB
=>AB^2=AD*AE
Xét (O) có
AB,AC là tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc với BC
=>AH*AO=AB^2=AE*AD
Y
22 tháng 3 2022
\(a,\) Ta có :
\(OB=OC=R\)
\(AB=AC\) (t/c 2 tiếp tuyến cắt nhau)
\(\Rightarrow OA\) là đường trung trực của \(BC\)
\(\Rightarrow OA\perp BC\)
\(b,\) Xét \(\Delta ABE\) và \(\Delta ABD\) có :
\(\widehat{BAE}\) chung
\(\widehat{BED}=\widehat{ABD}\) (cùng chắn \(\stackrel\frown{BD}\) )
\(\Rightarrow\Delta ABE\sim\Delta ABD\left(g-g\right)\)
\(\Rightarrow\dfrac{AB}{AD}=\dfrac{AE}{AB}\)
\(\Rightarrow AB^2=AD.AE\)
Y
22 tháng 3 2022
Xét \(\Delta OAB\perp\) tại \(A\) có :
\(AB^2=AH.AO\left(HTL\right)\) \(\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\Rightarrow\) \(AD.AE=AH.AO\)
Xét \(\Delta AHD\) và \(\Delta AEO\) có :
\(\widehat{OAE}chung\)
\(\dfrac{AD}{AH}=\dfrac{AO}{AE}\left(AD.AE=AH.AO\right)\)
\(\Rightarrow\Delta AHD\sim\Delta AEO\left(c-g-c\right)\)
\(\Rightarrow\widehat{AHD}=\widehat{AEO}\)
\(\Rightarrow\) Tứ giác \(DHOE\) nội tiếp (góc ngoài = góc đối trong)
31 tháng 7 2023
\(A=\sqrt{3-\sqrt{5}}-\sqrt{4-\sqrt{15}}+\sqrt{6-3\sqrt{3}}\)
\(=\dfrac{1}{\sqrt{2}}\cdot\left(\sqrt{6-2\sqrt{5}}-\sqrt{8-2\sqrt{15}}+\sqrt{12-6\sqrt{3}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{5}-1-\sqrt{5}+\sqrt{3}+3-\sqrt{3}\right)\)
=2/căn 2=căn 2
\(B=\sqrt{4-\sqrt{7}}-\sqrt{14-5\sqrt{3}}-\sqrt{5+\sqrt{21}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{8-2\sqrt{7}}-\sqrt{28-10\sqrt{3}}-\sqrt{10+2\sqrt{21}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{7}-1-5+\sqrt{3}-\sqrt{7}-\sqrt{3}\right)\)
=-6/căn 2=-3căn2
\(C=\sqrt{11-6\sqrt{2}}-\sqrt{6-4\sqrt{2}}+\sqrt{7-2\sqrt{6}}\)
=3-căn 2-2+căn 2+căn 6-1
=căn 6
\(D=\sqrt{6-\sqrt{11}}-\sqrt{10+3\sqrt{11}}+2\sqrt{2}-1\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{12-2\sqrt{11}}-\sqrt{20+6\sqrt{11}}\right)+2\sqrt{2}-1\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{11}-1-\sqrt{11}-3\right)+2\sqrt{2}-1\)
=-1
\(F=\sqrt{6+3\sqrt{3}}-\sqrt{2+\sqrt{3}}+\sqrt{6-4\sqrt{2}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{12+6\sqrt{3}}-\sqrt{4+2\sqrt{3}}\right)+2-\sqrt{2}\)
=1/căn 2(3+căn 3-căn 3-1)+2-căn 2
=căn 2+2-căn 2
=2
TR
1
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 2 2022
5.
\(\Delta=\left(-2\right)^2-4\left(-15\right)=64\)
6.
\(\Delta'=2^2-5.\left(-7\right)=39\)
8 tháng 2 2022
Mà thầy ơi em hok hiểu khúc đầu làm sao để ra cái đó ròi ra kết quả á :((( cả 2 câu lun
5 tháng 12 2021
Đk: x>0, x≠1
P=(√x/(√x -1) +√x/(√x +1)):√(4x)/(x-1)
P=((x+√x)/(x-1)+(x-√x)/(x-1)).(x-1)/√(4x)
P=(x+√x + x-√x)/(x-1).(x-1)/√(4x)
P=(2x)/(x-1).(x-1)/√(4x)
P=(2x)/√(4x)
P=√x
Vậy P=√x
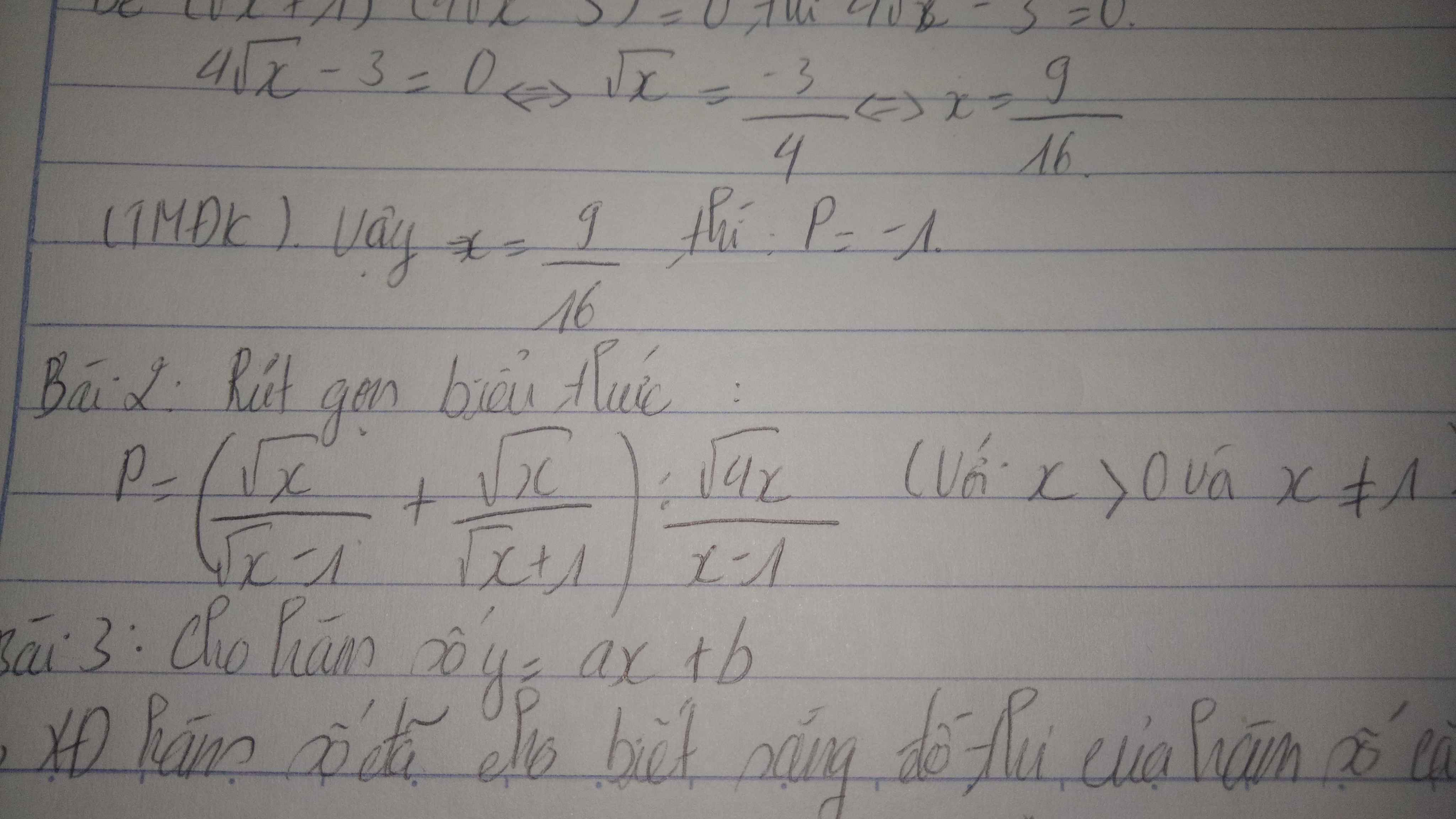
1: Gọi thể tích nước mỗi giờ phải bơm là x
Theo đề, ta có: 50/x-50/x+5=1+2/3=5/3
=>\(\dfrac{10}{x}-\dfrac{10}{x+5}=\dfrac{1}{3}\)
=>\(\dfrac{10x+50-10x}{x\left(x+5\right)}=\dfrac{1}{3}\)
=>x^2+5x-150=0
=>x=10