
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hình tròn bán kính R (ứng với cung 360o) có diện tích là πR2
Vậy hình quạt tròn bán kính R, cung 1o có diện tích là (πR2)/360
Hình quạt tròn bán kính R, cung no có diện tích S = (πR2n)/360

Hình tròn bán kính R (ứng với cung 360 ° ) có diện tích là π R 2
Vậy hình quạt tròn bán kính R, cung 1 ° có diện tích là π R 2 / 360
Hình quạt tròn bán kính R, cung n ° có diện tích S = π R 2 n / 360

Gọi x,y,z lần lượt là số đo độ của ba cung
ta có: x + y + z = 360 °
Theo đề bài ta có: 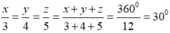
suy ra: x = 3. 30 ° = 90 ° ; y = 4. 30 ° = 120 ° ;z = 5. 30 ° = 150 °
Diện tích hình quạt tương ứng với các cung 90 ° , 120 ° , 150 ° là :
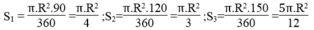

Gọi I,E,F lần lược là tiếp điểm của đường tròn tâm O nội tiếp với AB,BC,CA ta có OI = OE = OF = r
S ABC = S AOB + S BOC + S COA = AB.OI/2 + BC.OE/2 + CA.OF/2
= (AB + BC + CA).r/2 = pr
Gọi O là tâm đường tròn nội tiếp tam giác ABC
Nối OA, OB, OC
Khoảng cách từ tâm O đến các tiếp điểm là đường cao của các tam giác OAB, OAC, OBCv
Ta có : SABC = SOAB + SOAC + SOBC
\(=\left(\frac{1}{2}\right)AB.r+\left(\frac{1}{2}\right).AC.r+\left(\frac{1}{2}\right).BC.r\)
\(=\left(\frac{1}{2}\right)\left(AB+AC+BC\right).r\)
Mà AB + AC + BC = 2p
Nên \(S_{ABC}=\left(\frac{1}{2}\right).2p.r=p.r\)

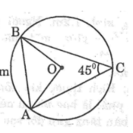
OM^2+ON^2=MN^2
OM=ON
=>ΔOMN vuông cân tại O
\(S_{q\left(OMN\right)}=\dfrac{pi\cdot3^2\cdot90}{360}=2.25pi\)
b: \(S_{OMN}=\dfrac{1}{2}\cdot OM\cdot ON=4.5\left(cm^2\right)\)
\(S_{VP\left(MN\right)}=2.25pi-4.5\)(cm2)
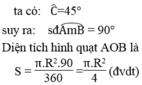
Diện tích hình quạt tròn có công thức là :
S = π.R².n/360 hay S = l.R/2
`S=(π R^2 n)/360`
`S=(lπ)/2`
.
n: số đo quạt tròn
l: độ dài cung `n^o`