Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có các khả năng sau
- Đoàn công tác gồm: 1 nhà toán học nữ, 1 nhà vật lý và 1 nhà toán học nam
Số cách chọn: C 7 1 . C 4 1 . C 5 1 = 140 cách
- Đoàn công tác gồm: 1 nhà toán học nữ, 2 nhà vật lý
Số cách chọn: C 4 1 . C 5 2 = 40 cách
- Đoàn công tác gồm: 2 nhà toán học nữ, 1 nhà vật lý
Số cách chọn: C 4 2 . C 5 1 = 30 cách
Vậy số cách lập là: 140 + 40 + 30 = 210 cách.
Chọn đáp án A.
Đáp án A.
* Hướng dẫn giải:
+ Đoàn công tác gồm: 1 nhà toán học nữ, 1 nhà vật lý và 1 nhà toán học nam
Số các để chọn: 
cách
+ Đoàn công tác gồm: 1 nhà toán học nữ, 2 nhà vật lý
Số cách chọn: 
cách
+ Đoàn công tác gồm: 2 nhà toán học nữ, 1 nhà vật lý
Số cách chọn: 
cách
Vậy số cách lập là: 210 cách
Đáp án B
Th1 : Số cách chọn ra 1 nhà toán học nam, 1 nhà toán học nữ, 1 nhà vật lý nam : 5.3.4 = 60
Th2 : Số cách chọn ra 2 nhà toán học nữ, 1 nhà vật lý nam : C 3 2 . C 4 1 = 12
Th3 : Số cách chọn ra 1 nhà toán học nữ, 2 nhà vật lý nam : C 3 1 C 4 2 = 18
Vậy có số cách chọn là : 90.
a.
Chọn 1 nam từ 9 nam có 9 cách
Chọn 1 nữ từ 3 nữ có 3 cách
\(\Rightarrow\) Có \(9.3=27\) cách chọn nhóm 1 nam 1 nữ
b.
Chọn 2 nhà toán học từ 8 nahf toán học: \(C_8^2\) cách
Chọn 2 nhà vật lý từ 4 nhà vật lý: \(C_4^2\) cách
\(\Rightarrow C_8^2.C_4^2\) cách lập
c.
Các trường hợp thỏa mãn: (1 nhà toán học nữ, 2 nhà vật lý nam), (1 nhà toán học nữ, 1 nhà toán học nam, 1 nhà vật lý nam), (2 nhà toán học nữ, 1 nhà vật lý nam)
\(\Rightarrow C_3^1.C_4^2+C_3^1.C_5^1.C_4^1+C_3^2.C_4^1\) cách
Đáp án B.
Số cách chọn 5 em học sinh từ 8 học sinh trên là 
cách
- Để chọn 5 em thỏa mãn bài ra, ta xét các trường hợp sau
+) 1 nam khối 11, 1 nữ khối 12 và 3 nam khối 12 có 
cách
+) 1 nam khối 11, 2 nữ khối 12 và 2 nam khối 12 có 
cách
+) 2 nam khối 11, 1 nữ khối 12 và 2 nam khối 12 có 
cách
+) 2 nam khối 11, 2 nữ khối 12 và 1 nam khối 12 có 
cách
- Số cách chọn 5 em thỏa mãn bài ra là:
cách
Vậy xác suất cần tính là: 
Có 7 nam chọn 5 em thì có C75 cách chọn, có 9 nữ chọn 5 nữ thì có C95 cách chọn. Sau đó Ta có 5! Cách ghép 5 nam và 5 nữ đã chọn.
Vậy có C75 . C95 .5!=317520 cách thỏa mãn yêu cầu bài toán.
Nhận xét. Những nhầm lẫn học sinh có thể tính ra kết quả
C75 . C95 =2646 ( phương án A) Do quan niệm ghép 5 nam,5 nữ thành cặp chỉ có một cách.
A75 .A95 =38102400( phương án C) Do quan niệm nhầm việc chọn 5 bạn trong 7 bạn (hoặc trong 9 bạn) là một chỉnh hợp chập 5 của 7( hoặc của 9)
Chọn B
Chọn B.
Số phần tử của không gian mẫu:
Gọi A là biến cố “nhóm được chọn có cả nam và nữ, đồng thời mỗi khối có 1 học sinh nam”
⇒ số phần tử của biến cố A là: 
.
Chọn C.
Số phần tử của của không gian mẫu: 
- Gọi A là biến cố: “Các giáo viên được chọn có 2 nam và 2 nữ”
Ta có các khả năng sau
Đoàn công tác gồm: 1 nhà toán học nữ, 1 nhà vật lý và 1 nhà toán học nam
Số cách chọn: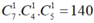
cách
Đoàn công tác gồm: 1 nhà toán học nữ, 2 nhà vật lý
Số cách chọn: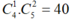
cách
Đoàn công tác gồm: 2 nhà toán học nữ, 1 nhà vật lý
Số cách chọn: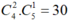
cách
Vậy số cách lập là: 210 cách.
Chọn A.