K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
2 tháng 5 2017
Sơ đồ con đường |
Lời giải chi tiết |
Áp dụng tính chất chia hết của một hiệu. |
Ta có: 36 ⋮ 9 ⇒ 36 36 ⋮ 9 9 ⋮ 9 ⇒ 9 10 ⋮ 9 ⇒ 36 36 + 9 10 ⋮ 9 |
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
24 tháng 12 2022
Đây bản chất là bài tìm ước của 3636 thôi em nhé. em viết số 3636 dưới dạng tích các thừa số nguyên tố là tìm được :
3636 = 22 . 32 . 101
Ư( 3636) = { 1; 2; 3; 4; 6; 9; 12; 18; 36; 101; 202; 303; 404; 606; 909; 1212; 1818; 3636}
Kết luận vậy 3636 chia hết cho các số :
1; 2; 3; 4; 6; 9; 12; 18; 36; 101; 202; 303; 404; 606; 909; 1212; 1818; 3636
N
0
TM
1
14 tháng 10 2017
a)vì 60.n chia hết cho 15
45 chia hết cho 15
=>60.n+45 chia hết cho 15
b)vì 60.n chia hết cho 30
45 ko chia hết cho 30
=>60.n +45 ko chia hết cho 30
23 tháng 7 2017
1)
a) 3636-(12x-9)=36
12x-9=3636-36
12x-9=3600
12x=3600+9
12x=3609
x=3609:12
x=\(30\dfrac{3}{40}\)
23 tháng 7 2017
1)
b) \(\left(\dfrac{x}{23}+45\right).67=8911\)
\(\dfrac{x}{23}+45=8911:67\)
\(\dfrac{x}{23}+45=133\)
\(x:23=133-45\)
\(x:23=88\)
\(x=88.23\)
\(x=2024\)
PD
1
HM
27 tháng 3 2018
Áp dụng hằng đẳng thức sau
an−1=(a−1).[an−1+an−2+...+1]=(a−1).pan−1=(a−1).[an−1+an−2+...+1]=(a−1).p (nn là 1 số nguyên dương)
an+1=(a+1).[an−1−an−2+..+1]=(a+1).qan+1=(a+1).[an−1−an−2+..+1]=(a+1).q (nn là 1 số nguyên dương lẻ)
Thay vào ta được như sau:
+) 222333−1=(222−1).p=13.17.p222333−1=(222−1).p=13.17.p
+) 333222+1=(3332)111+1=110889111+1=(110889+1).q=13.8530.q333222+1=(3332)111+1=110889111+1=(110889+1).q=13.8530.q
=>=> 222333+333222=222333−1+333222+1=13(17p+8530q)⋮13222333+333222=222333−1+333222+1=13(17p+8530q)⋮13
Vậy: 222333+333222⋮13222333+333222⋮13 (đpcm)(đpcm)
LH
2
20 tháng 9 2016
\(\left(222^{333}+333^{222}\right)⋮13\)
Áp dụng hằng đẳng thức sau
( là 1 số nguyên dương)
( là 1 số nguyên dương lẻ)
Thay vào ta được như sau:
+)
+)
20 tháng 9 2016
bác nên nhớ là lp 6 chưa hs hđt nhé nên ko đc áp dụng -_-
11 tháng 5 2022
Ta thấy số 2139 có tân cùng là 1; số 3921 có tận cùng là 9, vậy tổng 2139 + 3921 có tận cùng là 0, chia hết cho 5.
Lại có 2139 = (3.7)39 = 339.739 = 32(337.739) = 9. (337.739) chia hết cho 9
3921 = (3.13)21 = 32 (319.1321) = 9. (319.1321) chia hết cho 9
Vậy thì tổng 2139 + 3921 chia hết cho 9.
Do (5 ; 9) = 1 nên ta suy ra tổng 2139 + 3921 chia hết cho 45.
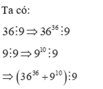
Ta có:
\(36^{36}-9^{10}⋮9\) vì các số hạng đều chia hết cho \(9\).
Mặt khác:
\(36^{36}\) có số tận cùng là số \(6\).
\(9^{10}=\left(9^2\right)^5=81^5\) có tận cùng là \(1\)
\(\Rightarrow36^{36}-9^{10}\) có tận cùng là \(6-1=5\)
\(\Rightarrow36^{36}-9^{10}⋮5\)
Mà \(5;9\) là hai snt cùng nhau
\(\Rightarrow36^{36}-9^{10}\) chia hết cho \(45\)