Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này khá dễ, bạn hãy theo dõi bài giải của mình nhé! ^^
Ta có :
220 đồng dư với 118 (mod 102) => 220^11969 đồng dư với 118 (mod 102)
119 đồng dư với 17 (mod 102) => 119^69220 đồng dư với 17 (mod 102)
69 đồng dư với 69 (mod 102) => 69^220119 đồng dư với 69 (mod 102)
=> 220^11969 + 119^69220 + 69^220119 đồng dư với (118 + 17 + 69) (mod 102)
=> 220^11069 + 119^69220 + 69^220119 chia hết cho 102
ko khó đâu bn - chỉ cần giả 1 cách đơn giản như sau : ![]()
220 = 0 ( mod2) \(\Rightarrow220^{11969}=0\)(mod2)
119 = 1 ( mod2) \(\Rightarrow119^{69220}=1\) ( mod2)
69 = -1 *(mod2) \(\Rightarrow69^{220119}=-1\)(mod2)
\(\Rightarrow A=0\)(mod2) hay A \(⋮\)2
Tương tự ta thấy : A \(⋮\)3 và A\(⋮\)17
Vì 2 .3 . 17 = 102
\(\Rightarrow\) A \(⋮\) 102 ( đpcm,)

=\(\frac{\left(-2\right)^8}{5^4}\times\frac{\left(-1\right)^2}{2^2}\div\frac{\left(-1\right)^3}{5^3}\)
=\(\frac{2^8}{5^4}\times\frac{1}{2^2}\times\frac{-5^3}{1}\)
=\(\frac{-64}{5}\)

\(=\dfrac{\left(20\cdot16-12\cdot8-48\cdot4\right)^2}{-2^9}=\dfrac{2^{10}}{-2^9}=-2\)

Trả lời :
\(\frac{27^2}{25^3}\)
\(=\frac{729}{15625}\)
\(=0,46656\)

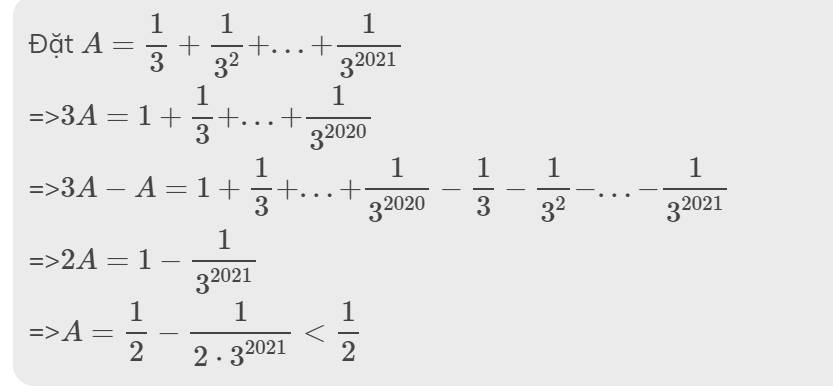
Đặt \(A=\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{2021}}\)
=>\(3A=1+\dfrac{1}{3}+...+\dfrac{1}{3^{2020}}\)
=>\(3A-A=1+\dfrac{1}{3}+...+\dfrac{1}{3^{2020}}-\dfrac{1}{3}-\dfrac{1}{3^2}-...-\dfrac{1}{3^{2021}}\)
=>\(2A=1-\dfrac{1}{3^{2021}}\)
=>\(A=\dfrac{1}{2}-\dfrac{1}{2\cdot3^{2021}}< \dfrac{1}{2}\)
xin lỗi mik mới lên lớp 7 chưa học tới bài này! thông cảm