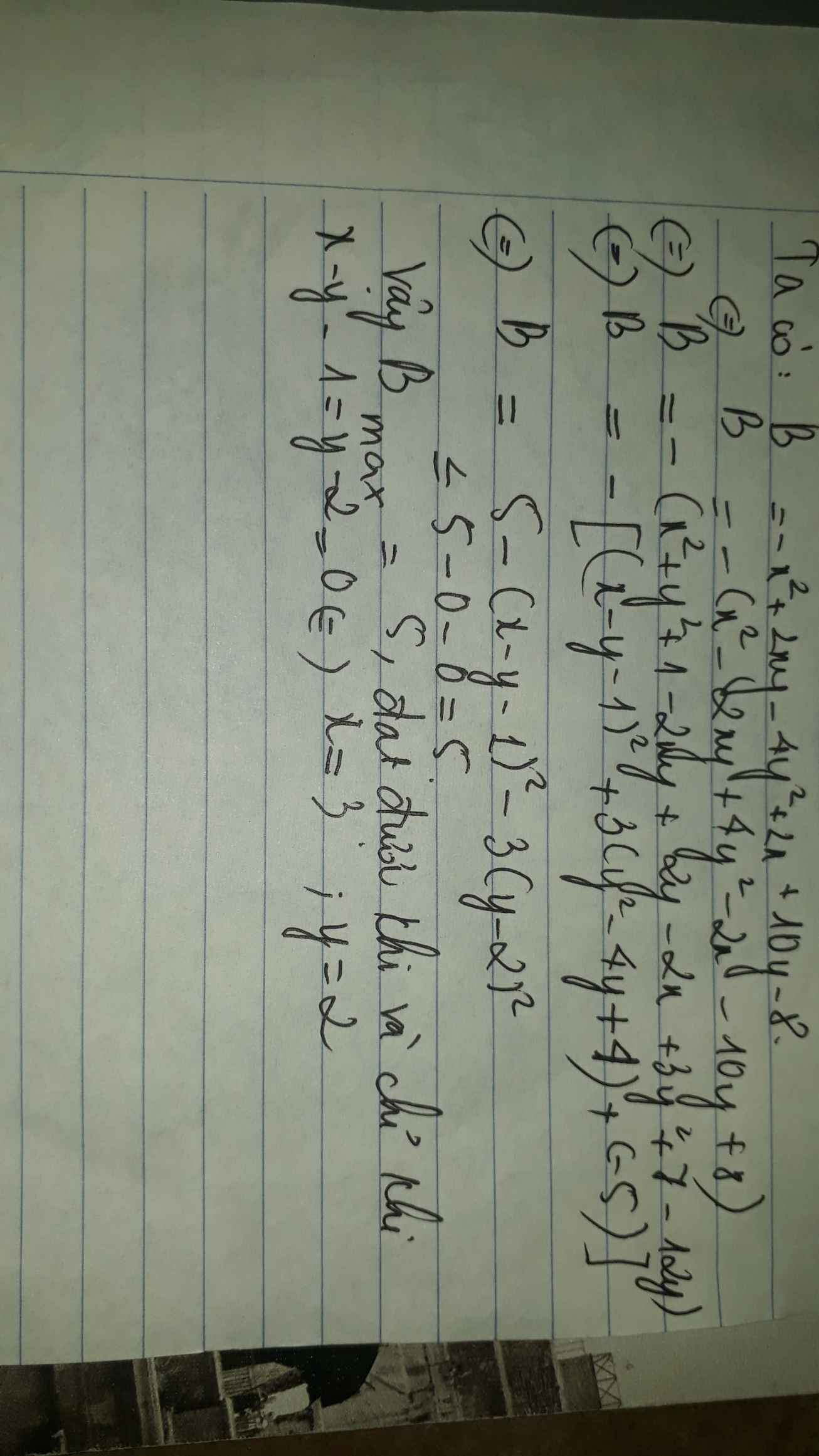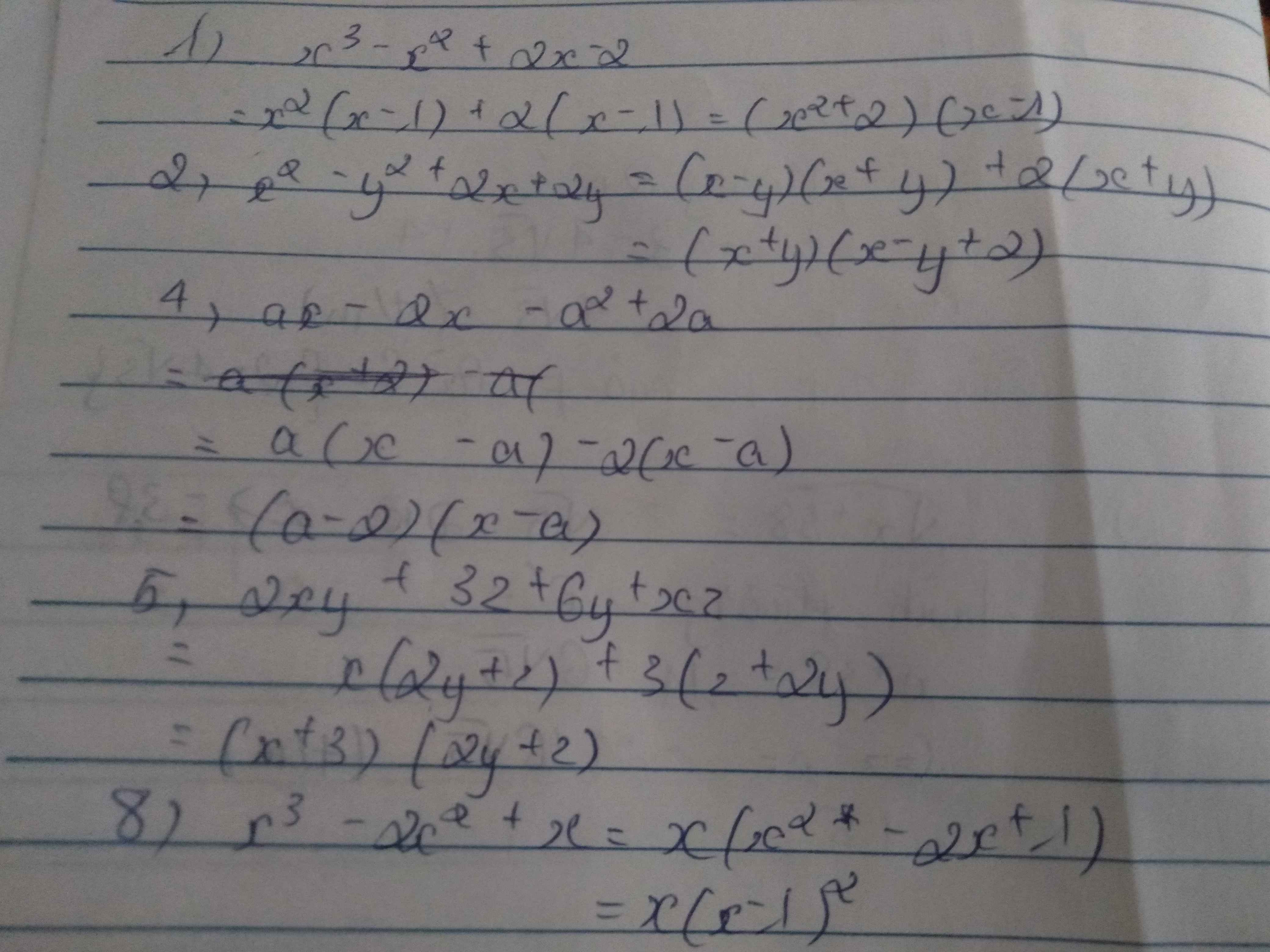K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
0
19 tháng 12 2020
A= -x2+2x+3
=>A= -(x2-2x+3)
=>A= -(x2-2.x.1+1+3-1)
=>A=-[(x-1)2+2]
=>A= -(x+1)2-2
Vì -(x+1)2 ≤0=> A≤-2
Dấu "=" xảy ra khi
-(x+1)2=0 => x=-1
Vây A lớn nhất= -2 khi x= -1
19 tháng 12 2020
B=x2-2x+4y2-4y+8
=> B= (x2-2x+1)+(4y2-4y+1)+6
=> B=(x-1)2+(2y+1)2+6
=> B lớn nhất=6 khi x=1 và y=-1/2
AH
Akai Haruma
Giáo viên
24 tháng 11 2021
a.
$12x^3y-24x^2y^2+12xy^3=12xy(x^2-2xy+y^2)=12xy(x-y)^2$
b.
$x^2-6x+xy-6y=(x^2+xy)-(6x+6y)=x(x+y)-6(x+y)=(x-6)(x+y)$
c.
$2x^2+2xy-x-y=2x(x+y)-(x+y)=(x+y)(2x-1)$
d.
$x^3-3x^2+3x-1=(x-1)^3$
e.
$3x^2-3y^2-12x-12y=(3x^2-3y^2)-(12x+12y)$
$=3(x-y)(x+y)-12(x+y)=(x+y)[3(x-y)-12]=3(x-y)(x-y-4)$
f.
$x^2-2xy-x^2+4y^2=4y^2-2xy=2y(2y-x)$
BS
1
28 tháng 8 2018
\(A=-x^2+2xy-4y^2+2x+10y-8\)
\(=-\left(x^2-2xy+4y^2-2x-10y+8\right)\)
\(=-\left[\left(x-y-1\right)^2+3\left(y-2\right)^2-5\right]\)
\(=5-\left(x-y-1\right)^2-3\left(y-2\right)^2\le5\)
Dấu"=" xảy ra <=> \(\hept{\begin{cases}x-y-1=0\\y-2=0\end{cases}}\) <=> \(\hept{\begin{cases}x=3\\y=2\end{cases}}\)
Vậy MAX \(A=5\)khi \(x=3;\)\(y=2\)
KB
28 tháng 8 2018
\(-x^2+2xy-4y^2+2x+10y-8\)
\(=-\left(x^2-2xy+y^2\right)+2\left(x-y\right)+12y-8-3y^2\)
\(=-\left(x-y\right)^2+2\left(x-y\right)-3\left(y^2-4y+4\right)+4\)
\(=-\left[\left(x-y\right)^2-2\left(x-y\right)+1\right]-3\left(y-2\right)^2+5\)
\(=-\left(x-y-1\right)^2-3\left(y-2\right)^2+5\)
\(=-\left[\left(x-y-1\right)^2+3\left(y-2\right)^2\right]+5\le5\forall x;y\)
Dấu " = " xảy ra
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-y-1\right)^2=0\\3\left(y-2\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y-1=0\\\left(y-2\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-y=1\\y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y+1\\y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2\end{matrix}\right.\)
Vậy GTLN của biểu thức trên là : \(5\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2\end{matrix}\right.\)