
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a. $3(x-\frac{1}{2})-3(x-\frac{1}{3})=x$
$3[(x-\frac{1}{2})-(x-\frac{1}{3})]=x$
$3.\frac{-1}{6}=x$
$\Rightarrow x=\frac{-1}{2}$
b.
$\frac{1}{2}(x+2)-4(x-\frac{1}{4})=\frac{1}{2}x$
$\frac{1}{2}x+1-4(x-\frac{1}{4})=\frac{1}{2}x$
$1-4(x-\frac{1}{4})=0$
$x-\frac{1}{4}=\frac{1}{4}$
$x=\frac{1}{4}+\frac{1}{4}=\frac{1}{2}$

a, \(M=2x^4y^3-\dfrac{1}{5}xy-xy^3\)
bậc 7
b, Thay x = -2,5 ; y = 0,4 vào ta được
\(2\left(-2,5\right)^4.0,4^3-\dfrac{1}{5}\left(-2,5\right).0,4+2,5.\left(0,4\right)^3=5,36\)

a, \(\dfrac{15}{4}\) - 2,5 : |\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 3
3,75 - 2,5:|\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 3
2,5:|\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 3,75 - 3
2,5 : |\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 0,75
|\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 2,5 : 0,75
|\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = \(\dfrac{10}{3}\)
\(\left[{}\begin{matrix}\dfrac{3}{4}x+\dfrac{1}{2}=-\dfrac{10}{3}\\\dfrac{3}{4}x+\dfrac{1}{2}=\dfrac{10}{3}\end{matrix}\right.\)
\(\left[{}\begin{matrix}\dfrac{3}{4}x=-\dfrac{10}{3}-\dfrac{1}{2}\\\dfrac{3}{4}x=\dfrac{10}{3}-\dfrac{1}{2}\end{matrix}\right.\)
\(\left[{}\begin{matrix}\dfrac{3}{4}x=-\dfrac{26}{3}\\\dfrac{3}{4}x=\dfrac{17}{6}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-\dfrac{46}{9}\\x=\dfrac{34}{9}\end{matrix}\right.\)

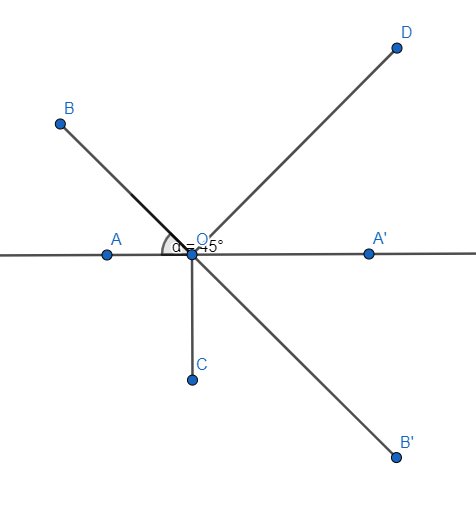
a) Vì OB' là tia phân giác của \(\widehat{A'OC}\) nên \(\widehat{A'OB'}=\dfrac{\widehat{A'OC}}{2}=\dfrac{90^o}{2}=45^o\). Suy ra \(\widehat{AOB}=\widehat{A'OB'}\left(=45^o\right)\). Lại có \(\widehat{AOB}+\widehat{BOA'}=\widehat{AOA'}=180^o\) nên \(\widehat{BOB'}=\widehat{A'OB'}+\widehat{BOA'}=180^o\) hay B, O, B' thẳng hàng. Suy ra \(\widehat{AOB}\) và \(\widehat{A'OB'}\) là 2 góc đối đỉnh.
b) Trên cùng 1 nửa mặt phẳng bờ là đường thẳng AA', ta thấy tia OB nằm giữa 2 tia OA và OD, tia OD lại nằm giữa 2 tia OB và OA', do đó \(\widehat{AOB}+\widehat{BOD}+\widehat{DOA'}=\widehat{AOA'}\) \(\Leftrightarrow45^o+90^o+\widehat{A'OD}=180^o\) \(\Leftrightarrow\widehat{A'OD}=45^o\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{a+b}{3+5}=\dfrac{160000000}{8}=20000000\)
Do đó: a=60000000; b=100000000

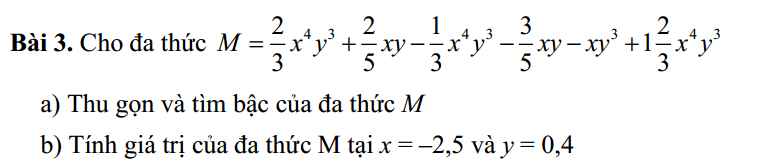

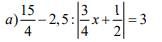 Cíu mình với=(((
Cíu mình với=(((
5p' zì cơ:)?
C