
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


*Sửa lại đề*
A = 21+ 22+ 23+ 24 + .. + 2100
A = (21+22) + (23+ 24) +...+ (299+ 2100)
A = 2.(1+2) + 23.(1+2) + .. + 299. (1+2)
A = 2.3 + 23. 3 + .. + 299.3
A = 3 . (21 + 23 + .... + 299)
Mà 3 chia hết cho 3
=> A chia hết cho 3


Lời giải:
a, Ta có: \(A=\frac{1}{12}+\frac{1}{13}+\frac{1}{14}+\frac{1}{15}+...+\frac{1}{22}>\frac{1}{22}+\frac{1}{22}+\frac{1}{22}+\frac{1}{22}+...+\frac{1}{22}=\frac{1}{22}.11=\frac{11}{22}=\frac{1}{2}\)
Vậy: \(A>\frac{1}{2}\)
b, Ta có: \(B=\frac{1}{10}+\frac{1}{11}+\frac{1}{12}+\frac{1}{13}+...+\frac{1}{99}+\frac{1}{100}\)
\(=\left(\frac{1}{10}+\frac{1}{11}+...+\frac{1}{49}+\frac{1}{50}\right)+\left(\frac{1}{51}+\frac{1}{52}+...+\frac{1}{99}+\frac{1}{100}\right)\)
Mà: \(\left(\frac{1}{10}+\frac{1}{11}+...+\frac{1}{49}+\frac{1}{50}\right)+\left(\frac{1}{51}+\frac{1}{52}+...+\frac{1}{99}+\frac{1}{100}\right)\text{}\text{}\text{}>\left(\frac{1}{50}+...+\frac{1}{50}+\frac{1}{50}\right)+\left(\frac{1}{100}+...+\frac{1}{100}+\frac{1}{100}\right)\)
=> \(B\text{}\text{}\text{}>\frac{1}{50}.41+\frac{1}{100}.50=\frac{41+25}{50}=\frac{33}{25}>1\)
Vậy: \(B>1\)
c, Ta có: \(C=\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+...+\frac{1}{16}+\frac{1}{17}< \frac{1}{5}+\frac{1}{6}+\left(\frac{1}{7}+...+\frac{1}{7}+\frac{1}{7}\right)=\frac{11}{30}+11.\frac{1}{7}=\frac{407}{210}< \frac{420}{210}=2\)
Vậy: \(C< 2\)
![]() Chúc bạn học tốt!
Chúc bạn học tốt!![]() Tick cho mình nhé!
Tick cho mình nhé!![]()


\(A.x=x+x^2+x^3+...+x^{101}\)
\(A.x-A=x^{101}-1\Rightarrow A\left(x-1\right)=x^{101}-1\)
\(\Rightarrow A=\dfrac{x^{101}-1}{x-1}\)

Bài 1:
13 + 23 = 1 + 8 = 9 = 32 (là một số chính phương)
13 + 23 + 33 = 1 + 8 + 27 = 36 = 62 (là một số chính phương)
13 + 23 + 33 + 43 = 1 + 8 + 27 + 64 = 100 = 102 (là số cp)
13 + 23 + 33 + 43 + 53 = 1 + 8 + 27 + 64 + 125 = 225 = (15)2 là số cp
Bài 2:
1262 + 1 = \(\overline{..6}\) + 1 = \(\overline{...7}\) (không phải số chính phương)
100! + 8 = \(\overline{...0}\) + 8 = \(\overline{...8}\) (không phải là số chính phương)
1012 - 3 \(\overline{..01}\) - 3 = \(\overline{...8}\) (không phải là số chính phương)
107 + 7 = \(\overline{..0}\) + 7 = \(\overline{..7}\) (không phải là số chính phương)
11 + 112 + 113 = \(\overline{..1}\)+ \(\overline{..1}\)+ \(\overline{..1}\) = \(\overline{...3}\) (không phải số chính phương)

\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{99}}\)
\(\Rightarrow\dfrac{A}{3}=\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\)
\(\Rightarrow A-\dfrac{A}{3}=\dfrac{2A}{3}=\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}\right)-\left(\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\dfrac{2A}{3}=\left(\dfrac{1}{3^2}-\dfrac{1}{3^2}\right)+\left(\dfrac{1}{3^3}-\dfrac{1}{3^3}\right)+...+\left(\dfrac{1}{3^{99}}-\dfrac{1}{3^{99}}\right)+\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)=\dfrac{1}{3}-\dfrac{1}{3^{100}}\)
\(\Rightarrow2A=3\cdot\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\text{A}=\dfrac{1-\dfrac{1}{3^{99}}}{2}\)
\(\Rightarrow A=\dfrac{1}{2}-\dfrac{1}{2.3^{99}}< \dfrac{1}{2}\)
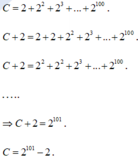
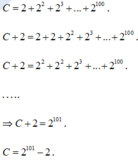
\(A=\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^2}+....+\frac{100}{2^{100}}\)
\(\Rightarrow2A=1+\frac{2}{2}+\frac{3}{2^2}+...+\frac{100}{2^{99}}\)
\(\Rightarrow2A-A=1+\frac{2}{2}+\frac{3}{2^2}+...+\frac{100}{2^{99}}-\frac{1}{2}-\frac{2}{2^2}-...-\frac{100}{2^{100}}\)
\(\Rightarrow A=1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{99}}-\frac{100}{2^{100}}\)
\(\Rightarrow A< 1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{99}}\)(3)
Đặt \(P=1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{99}}\)(2)
\(\Rightarrow2P=2+1+\frac{1}{2}+...+\frac{1}{2^{98}}\)
\(\Rightarrow2P-P=2+1+\frac{1}{2}+...+\frac{1}{2^{98}}-1-\frac{1}{2}-...-\frac{1}{2^{99}}\)
\(\Rightarrow P=2-\frac{1}{2^{99}}< 2\)(1)
Từ (1),(2),(3) => A<2
Giải
Ta có A =1/2 + 2/2^2 + 3/2^3 + ... + 100/2^100
=> 2A = 1 + 2/2 + 3/2^2 + ... + 100/2^99
=> 2A - A = 1 + 1/2 + 1/2^2 + 1/2^3 + ... + 1/2^99 - 100/2^100
=> A = ( 1 - 100/2^100) + 1/2 + 1/2^2 + 1/2^3 + ... + 1/2^99 (*)
Đặt B = 1/2 + 1/2^2 + 1/2^3 + ... + 1/2^99
=> 2B = 1 + 1/2 + 1/2^2 + ... + 1/2^98
=> 2B - B = 1 - 1/2^99
=> B = 1 - 1/2^99
Thay B vào (*) ta được:
A = ( 1 - 100/2^100 ) + ( 1 - 1/2^99 )
A = 2 - ( 100/2^100 + 1/2^99 ) < 2
=> A < 2 (đpcm)