Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ \(VT=\frac{\sin^4x+2\sin x.\cos x-\left(1-\sin^2x\right)^2}{\frac{\sin2x}{\cos2x}-1}\)
\(=\frac{\sin^4x+2\sin x.\cos x-1+2\sin^2x-\sin^4x}{\frac{\sin2x-\cos2x}{\cos2x}}\) \(=\frac{1-2\sin^2x-\sin2x}{\frac{\cos2x-\sin2x}{\cos2x}}=\frac{\cos2x-\sin2x}{\frac{\cos2x-\sin2x}{\cos2x}}=\cos2x=VP\)

Áp dụng công thức biến tích thành tổng:
\(cos\left(a+b\right).cos\left(a-b\right)=\dfrac{1}{2}\left(cos2a+cos2b\right)\)
\(=\dfrac{1}{2}\left(2cos^2a-1+1-2sin^2b\right)=\dfrac{1}{2}\left(2cos^2a-2sin^2b\right)\)
\(=cos^2a-sin^2b\)
\(cos\left(\dfrac{\pi}{4}+a\right).cos\left(\dfrac{\pi}{4}-a\right)+\dfrac{1}{2}sin^2a=\dfrac{1}{2}\left(cos\dfrac{\pi}{2}+cos2a\right)+\dfrac{1}{2}sin^2a\)
\(=\dfrac{1}{2}cos2a+\dfrac{1}{2}sin^2a=\dfrac{1}{2}\left(cos^2a-sin^2a\right)+\dfrac{1}{2}sin^2a\)
\(=\dfrac{1}{2}cos^2a\)

\(\dfrac{\sin^2a-\tan^2a}{\cos^2a-\cot^2a}=\dfrac{\sin^2a-\dfrac{\sin^2a}{\cos^2a}}{\cos^2a-\dfrac{\cos^2a}{\sin^2a}}=\dfrac{\dfrac{\sin^2a\cos^2a-\sin^2a}{\cos^2a}}{\dfrac{\cos^2a\sin^2a-\cos^2a}{\sin^2a}}=\dfrac{\sin^2a\sin^2a\left(\cos^2a-1\right)}{\cos^2a\cos^2a\left(\sin^2a-1\right)}\)
\(=\dfrac{\sin^4a\left(\cos^2a-\cos^2a-\sin^2a\right)}{\cos^4a\left(\sin^2a-\cos^2a-\sin^2a\right)}=\dfrac{\sin^4a\left(-\sin^2a\right)}{\cos^4a\left(-\cos^2a\right)}\)
\(=\dfrac{-\sin^6a}{-\cos^6a}=\dfrac{\sin^6a}{\cos^6a}=\tan^6a\)

a.
\(tana=\dfrac{sina}{cosa}=\dfrac{1}{15}\Rightarrow sina=\dfrac{cosa}{15}\)
\(\Rightarrow sin2a=2sina.cosa=\dfrac{2cosa}{15}.cosa=\dfrac{2}{15}cos^2a=\dfrac{2}{15}.\dfrac{1}{1+tan^2a}=\dfrac{2}{15}.\dfrac{1}{1+\dfrac{1}{15^2}}=\dfrac{15}{113}\)
b.
\(5^2=\left(3sina+4cosa\right)^2\le\left(3^2+4^2\right)\left(sin^2+cos^2a\right)=25\)
Đẳng thức xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}\dfrac{sina}{3}=\dfrac{cosa}{4}\\3sina+4cosa=5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}sina=\dfrac{3}{5}\\cosa=\dfrac{4}{5}\end{matrix}\right.\)
c.
\(\dfrac{1}{tan^2a}+\dfrac{1}{cot^2a}+\dfrac{1}{sin^2a}+\dfrac{1}{cos^2a}=7\)
\(\Leftrightarrow\dfrac{cos^2a}{sin^2a}+\dfrac{sin^2a}{cos^2a}+\dfrac{1}{sin^2a}+\dfrac{1}{cos^2a}=7\)
\(\)\(\Leftrightarrow\dfrac{sin^4a+cos^4a}{sin^2a.cos^2a}+\dfrac{sin^2a+cos^2a}{sin^2a.cos^2a}=7\)
\(\Leftrightarrow\dfrac{\left(sin^2a+cos^2a\right)^2-2sin^2a.cos^2a}{sin^2a.cos^2a}+\dfrac{1}{sin^2a.cos^2a}=7\)
\(\Leftrightarrow\dfrac{2}{sin^2a.cos^2a}=9\)
\(\Leftrightarrow\dfrac{8}{\left(2sina.cosa\right)^2}=9\)
\(\Leftrightarrow\dfrac{8}{sin^22a}=9\)
\(\Leftrightarrow sin^22a=\dfrac{8}{9}\)

Câu a)
Từ \(\tan a=3\Leftrightarrow \frac{\sin a}{\cos a}=3\Rightarrow \sin a=3\cos a\)
Do đó:
\(\frac{\sin a\cos a+\cos ^2a}{2\sin ^2a-\cos ^2a}=\frac{3\cos a\cos a+\cos ^2a}{2(3\cos a)^2-\cos ^2a}\)
\(=\frac{\cos ^2a(3+1)}{\cos ^2a(18-1)}=\frac{4}{17}\)
Câu b)
Có: \(\cot \left(\frac{\pi}{2}-x\right)=\tan x=\frac{\sin x}{\cos x}\)
\(\cos\left(\frac{\pi}{2}+x\right)=-\sin x\)
\(\Rightarrow \cot \left(\frac{\pi}{2}-x\right)\cos \left(\frac{\pi}{2}+x\right)=\frac{-\sin ^2x}{\cos x}\)
Và:
\(\frac{\sin (\pi-x)\cot x}{1-\sin ^2x}=\frac{\sin x\cot x}{\cos^2x}=\frac{\sin x.\frac{\cos x}{\sin x}}{\cos^2x}=\frac{1}{\cos x}\)
Do đó:
\(\Rightarrow \cot \left(\frac{\pi}{2}-x\right)\cos \left(\frac{\pi}{2}+x\right)+\frac{\sin (\pi-x)\cot x}{1-\sin ^2x}=\frac{1-\sin ^2x}{\cos x}=\frac{\cos ^2x}{\cos x}=\cos x\)
Ta có đpcm.
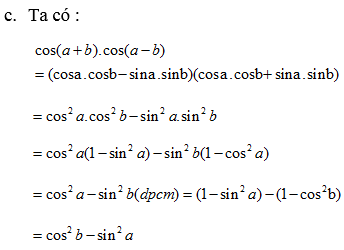


\(VT=\dfrac{sin^23a.cos^2a-sin^2a.cos^23a}{\left(sina.cosa\right)^2}\)
\(=\dfrac{\left(sin3a.cosa-sina.cos3a\right)\left(sin3a.cosa+sina.cos3a\right)}{\dfrac{1}{4}sin^22a}\)
\(=\dfrac{4sin2a.sin4a}{sin^22a}=\dfrac{4sin4a}{sin2a}=\dfrac{8.sin2a.cos2a}{sin2a}=8cos2a\)