
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

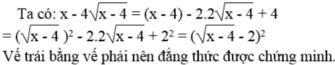



\(P=\left(\dfrac{\sqrt[4]{x^2}-\sqrt[4]{x}}{1-\sqrt[4]{x}}+\dfrac{1+\sqrt{x}}{\sqrt[4]{x}}\right)^2-\dfrac{\sqrt{1+\dfrac{2}{\sqrt{x}}+\dfrac{1}{x}}}{1+\sqrt{x}}\)
\(=\left(\dfrac{\sqrt[4]{x}\left(\sqrt[4]{x}-1\right)}{1-\sqrt[4]{x}}+\dfrac{1+\sqrt{x}}{\sqrt[4]{x}}\right)^2-\dfrac{\sqrt{\left(\dfrac{1}{\sqrt{x}}+1\right)^2}}{1+\sqrt{x}}\)
\(=\left(-\sqrt[4]{x}+\dfrac{1+\sqrt{x}}{\sqrt[4]{x}}\right)^2-\dfrac{\dfrac{1}{\sqrt{x}}+1}{1+\sqrt{x}}\)
\(=\left(\dfrac{1}{\sqrt[4]{x}}\right)^2-\dfrac{\dfrac{\sqrt{x}+1}{\sqrt{x}}}{\sqrt{x}+1}=\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{x}}=0\)

Hằng đẳng thức ???
Áp dụng BĐT \(x^2+y^2\ge2xy\) ta có:
\(\frac{x^4+y^4}{2}\ge\frac{\left(x^2\right)^2+\left(y^2\right)^2}{2}\ge\frac{2x^2y^2}{2}=x^2y^2\)
Tương tự cho 2 BĐT còn lại cũng có;
\(\frac{y^4+z^4}{2}\ge y^2z^2;\frac{z^4+x^4}{2}\ge x^2z^2\)
Cộng theo vế 3 BĐT trên ta có:
\(VT=\frac{x^4+y^4}{2}+\frac{y^4+z^4}{2}+\frac{z^4+x^4}{2}\ge x^2y^2+y^2z^2+z^2x^2=VP\)
Khi \(x=y=z\)
Áp dụng bđt Cô si cho 2 số không âm, ta có:
\(\hept{\begin{cases}\frac{x^4+y^4}{2}\ge\sqrt{x^4y^4}=x^2y^2\\\frac{y^4+z^4}{2}\ge\sqrt{y^4z^4}=y^2z^2\\\frac{z^4+x^4}{2}\ge\sqrt{z^4x^4}=z^2x^2\end{cases}}\)
\(\Rightarrow\frac{x^4+y^4}{2}+\frac{y^4+z^4}{2}+\frac{z^4+x^4}{2}\ge x^2y^2+y^2z^2+z^2x^2\)

Ta có:
x + 2 2 x - 4 = 2 + x - 2 2
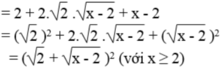
Vế trái bằng vế phải nên đẳng thức được chứng minh.

\(\left(\sqrt{x-\sqrt{x^2-4}}+\sqrt{x+\sqrt{x^2-4}}\right)^2=x-\sqrt{x^2-4}+2\sqrt{\left(x-\sqrt{x^2-4}\right)\left(x+\sqrt{x^2-4}\right)}\)
\(+x+\sqrt{x^2-4}=2x+2\sqrt{x^2-\left(x^2-4\right)}=2x+2\sqrt{x^2-x^2+4}=2x+2\sqrt{4}=2x+4\)
\(\Rightarrow\left(\sqrt{x-\sqrt{x^2-4}}+\sqrt{x+\sqrt{x^2-4}}\right)^2=2x+4\)
\(\Rightarrow\sqrt{x-\sqrt{x^2-4}}+\sqrt{x+\sqrt{x^2-4}}=\sqrt{2x+4}\)(đpcm)

mk làm lun nha
2 căn x-2+ căn x=4
3 căn x=6
căn x=2
x=4
**** cho mk nha

a, \(\sqrt{\left(\sqrt{5}-4\right)^2}-\sqrt{5}+\sqrt{20}=4\)
\(VT=\sqrt{\left(4-\sqrt{5}\right)^2}-\sqrt{5}+\sqrt{20}=\left|4-\sqrt{5}\right|-\sqrt{5}+\sqrt{20}\)
\(=4-\sqrt{5}-\sqrt{5}+2\sqrt{5}=4\) hay \(VT=VP\)
Vậy ta có đpcm
b, Với \(x>0,x\ne4\)
\(P=\left(\frac{1}{\sqrt{x}+2}+\frac{1}{\sqrt{x}-2}\right):\frac{2}{x-2\sqrt{x}}\)
\(=\left(\frac{\sqrt{x}-2+\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\right):\frac{2}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\frac{2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}.\frac{\sqrt{x}\left(\sqrt{x}-2\right)}{2}=\frac{x}{\sqrt{x}+2}\)
1.
Giả sử điều trên là đúng ta có:
\( \left | \sqrt{5}-4 \right |-\sqrt{5}+\sqrt{20}=4\)
Ta có: \(4>\sqrt{5}\)
\(\Rightarrow 4-\sqrt{5}- \sqrt{5}+\sqrt{20}=4\)
\(\Leftrightarrow 4-\sqrt{20}+\sqrt{20}=4\)
\(\Rightarrow đpcm\)
2.