Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cái nàyt nghĩ chỉ có cách quy đồng rồi chứng minh BĐT luôn đúng thôi bạn!
^_^

Không mất tính tổng quát giả sử \(a\ge b\ge c>0\Rightarrow\hept{\begin{cases}b+c\le a+c\le a+b\\\frac{a^a}{b+c}\ge\frac{b^a}{c+a}\ge\frac{c^a}{a+b}\end{cases}}\)
Sử dụng bất đẳng thức Chebyshev cho 2 dãy đơn ngược chiều ta có:
\(VT\left(1\right)=\frac{1}{2\left(a+b+c\right)}\left(\frac{a^a}{b+c}+\frac{b^a}{c+a}+\frac{c^a}{a+b}\right)\left[\left(b+c\right)+\left(c+a\right)+\left(a+b\right)\right]\ge\)
\(\frac{1}{2\left(a+b+c\right)}\cdot3\left[\frac{a^a}{b+c}\left(b+c\right)+\frac{b^a}{c+a}\left(c+a\right)+\frac{c^a}{a+b}\left(a+b\right)\right]=\frac{3\left(a^a+b^a+c^a\right)}{2\left(a+b+c\right)}\)\(=\frac{3}{2}\cdot\frac{a^a+b^a+c^a}{a+b+c}\)
=> đpcm

\(A=\left(a-b\right)^3+\left(b-c\right)^3+\left(c-a\right)^3\)
\(=a^3-3ab\left(a+b\right)+b^3+b^3-3bc\left(b+c\right)+c^3+c^3-3ca\left(c+a\right)+a^3\)
\(=3\left(a-b\right)\left(b-c\right)\left(c-a\right)\)\(⋮3\)
Lấy \(a,b,c\)lần lượt chia cho \(2\)ta được tối đa 2 số dư là: \(0;1\)Do đó tồn tại ít nhất 2 số có cùng số dư khi chia cho 2
\(\Rightarrow\)hiệu của chúng chia hết cho 2
\(\Rightarrow\)\(A⋮2\)
mà \(\left(2;3\right)=1\)\(\Rightarrow\)\(A⋮6\)

Điều kiện x ≠ 0 và x ≠ -3
Ta có:
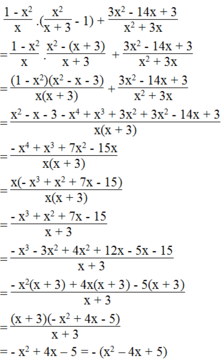
Vì x 2 - 4 x + 5 = x 2 - 4 x + 4 + 1 = x - 2 2 + 1 > 0 với mọi giá trị của x nên
- x 2 + 4 x - 5 = - x - 2 2 + 1 < 0 với mọi giá trị của x.
Vậy giá trị biểu thức luôn luôn âm với mọi giá trị x ≠ 0 và x ≠ -3

Ta chứng minh: \(a^3+b^3\ge ab\left(a+b\right)\)
Thực vậy, BĐT tương đương:
\(a^3+b^3-a^2b-ab^2\ge0\Leftrightarrow a^2\left(a-b\right)-b^2\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)\left(a^2-b^2\right)\ge0\Leftrightarrow\left(a-b\right)^2\left(a+b\right)\ge0\) (luôn đúng với a; b dương)
Vậy BĐT được chứng minh
Tương tự ta có: \(b^3+c^3\ge bc\left(b+c\right)\); \(c^3+a^3\ge ca\left(c+a\right)\)
Cộng vế với vế:
\(2\left(a^3+b^3+c^3\right)\ge ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)\)
\(\Rightarrow\frac{a^3+b^3+c^3}{ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)}\ge\frac{a^3+b^3+c^3}{2\left(a^3+b^3+c^3\right)}=\frac{1}{2}\)
Dấu "=" xảy ra khi \(a=b=c\)

Áp dụng bđt Cauchy Schwarz dạng Engel ta có:
\(\frac{a^2+b^2+c^2}{3}=\)(\(\frac{a^2}{1}+\frac{b^2}{1}+\frac{c^2}{1}\)).\(\frac{1}{3}\ge\)\(\frac{\left(a+b+c\right)^2}{1+1+1}.\frac{1}{3}=\)\(\left(\frac{a+b+c}{3}\right)^2\)(đpcm)
Dấu "=" xảy ra khi a = b = c
Đặt A = a + b, B = c. Áp dụng hằng đẳng thức ( A + B ) 3 để biến đổi vế trái.