Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

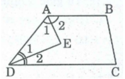
Giả sử hình thang ABCD có AB // CD
* Ta có: ∠ A 1 = ∠ A 2 = 1/2 ∠ A (vì AE là tia phân giác của góc A)
∠ D 1 = ∠ D 2 = 1/2 ∠ D ( Vì DE là tia phân giác của góc D)
Mà ∠ A + ∠ D = 180 0 (2 góc trong cùng phía bù nhau)
Suy ra: ∠ A 1 + ∠ D 1 = 1/2 ( ∠ A + ∠ D) = 90 0
* Trong ΔAED, ta có:
∠ (AED) + ∠ A 1 + ∠ D 1 = 180 0 (tổng 3 góc trong tam giác)
⇒ ∠ (AED) = 180 0 – ( ∠ A 1 + ∠ D 1 ) = 180 0 - 90 0 = 90 0
Vậy AE ⊥ DE.



nên \(\widehat{A}_1+\widehat{D}_1=90^0\). \(\Delta ADE\) có \(\widehat{A}_1+\widehat{D}_1=90^0\) nên \(\widehat{AED}=90^0\). Vậy \(AE\perp DE\)

Giải sử hình thang ABCD có AB// CD
\(\widehat{A_1}=\widehat{A_2}=\dfrac{1}{2}\widehat{A}\left(gt\right)\)
\(\widehat{D_1}=\widehat{D_2}=\dfrac{1}{2}\widehat{D}\left(gt\right)\)
Mà \(\widehat{A}+\widehat{D}=180^o\) (hai góc trong cùng phía bù nhau)
Suy ra:
\(\widehat{A}_1+\widehat{D_1}=\dfrac{1}{2}\left(\widehat{A}+\widehat{D}\right)=\dfrac{1}{2}.180^o=90^o\)
Trong ∆ AED ta có :
\(\widehat{AED}+\widehat{A_1}+\widehat{D_1}=180^o\) (tổng ba góc trong 1 tam giác)
\(\Rightarrow\widehat{AED}=180^o-\left(\widehat{A_1}+\widehat{D_1}\right)=180^o-90^o=90^o\)
\(\Rightarrow AE\perp ED\)
Vậy trong hình thang các tia phân giác của hai góc nhọn kề một cạnh bên vuông góc với nhau

1 )
Xét hình thang ABCD (AB//CD)
góc A + góc D =180 độ (2 góc trong cùng phía )
góc B +góc C =180 độ
- Nếu góc A tù (> 90độ) => góc D nhọn
- Nếu góc B tú => góc C nhọn
=> hình thang có nhiều nhất 2 góc tù, có nhiều nhất 2 góc nhọn
2 ) Giả sử ABCD là hình thang có đáy AB//CD
Khi đó ta có góc A + góc D bằng 180 độ (2 góc kề 1 cạnh bên hình thang bù nhau) (Hoặc bạn hiểu là 2 góc trong cùng phía bù nhau đó)
Vậy tia phân giác góc A nên bằng nửa góc A
TIa phân giác góc D bằng nửa góc D
Vậy Cộng 2 góc tia phân giác đó bằng 180độ chia 2 bằng 90 độ
2,
Giả sử ABCD là hình thang có đáy AB//CD
Khi đó ta có góc A + góc D bằng 180 độ (2 góc kề 1 cạnh bên hình thang bù nhau) (Hoặc bạn hiểu là 2 góc trong cùng phía bù nhau đó)
Vậy tia phân giác góc A nên bằng nửa góc A
TIa phân giác góc D bằng nửa góc D
Vậy Cộng 2 góc tia phân giác đó bằng 180 độ chia 2 bằng 90 độ

Ta có
\(\widehat{A}+\widehat{D}=180^o\) (Hai dt // bị cắt bởi 1 đường thẳng tạo thành 2 góc trong cùng phía bù nhau)
\(\widehat{DAE}=\frac{\widehat{A}}{2}\)
\(\widehat{ADE}=\frac{\widehat{D}}{2}\)
\(\Rightarrow\widehat{DAE}+\widehat{ADE}=\frac{\widehat{A}+\widehat{D}}{2}=\frac{180^o}{2}=90^o\)
Xét tg AED có
\(\widehat{DAE}+\widehat{ADE}=90^o\Rightarrow\widehat{AED}=90^o\Rightarrow AE\perp DE\)

A = A1 + A2 = 2A1 = 2A2
D = D1 + D2 = 2D1 =2D2
mà A + D =180O => A1 +D1 = 90
Gọi 2 tia phân giac góc A và D cắt nhau tại K xet tg AKD có A+D = 90 => K =90 (dpcm)

Bn có thể Tham khảo ở đường link này :
https://baitapsgk.com/lop-8/sbt-toan-lop-8/cau-16-trang-81-sach-bai-tap-sbt-toan-8-tap-1-chung-minh-rang-trong-hinh-thang-cac-tia-phan-giac-cua-hai-goc-ke-mot.html

Gọi ht đó là ABCD nha , AE là phân giác A ; DE là phân GIÁC cắt nhau tại E
AB //CD => A + D = 180 ĐỘ
Ta có EAD = 1/2 A (AE là phân giác ) (2)
EDA = 1/2 D ( DE là phân giác ) (1)
Từ (1) và (2) => EAD + EDA = = 1/2 ( A + D ) = 1/2.180 = 90 độ
TAM giác EAD có EAD + EDA = 90 độ => AED = 90độ
Hay AE vuông góc với DE
Tương tự cm với tia phân giác B và C
Ta gọi góc vuông là O .
Kéo dài CO sao cho CO=OE.
Kéo dài DO sao cho DO=OF
Xét tam giác DOC và tam giác EOF có :
CO=OE(cmt)
DO=OF(cmt)
O1=O2(đđ)
=>tam giác DOC+tam giác EOF = 360 độ
Mà 2 tam giác cân=> 2 tam giác = 360độ =>O=E+F+D1+C1:2=>góc O:2=90 độ