K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
29 tháng 9 2018
Cho hai hàm số y = f(x) và y = g(x) xác định trên R. Đặt S(x) = f(x) + g(x) và P(x) = f(x) g(x).Xét các mệnh đề:i) Nếu y = f(x) và y = g(x) là những hàm số chẵn thì y = S(x) và y = P(x) cũng là những hàm số chẵnii) Nếu y = f(x) và y = g(x) là những hàm số lẻ thì y = S(x) là hàm số lẻ và y = P(x) là hàm số chẵniii) Nếu y = f(x) là hàm số chẵn, y = g(x) là hàm số lẻ thì y = P(x) là hàm số lẻSố mệnh đề...
Đọc tiếp

Cho hai hàm số y = f(x) và y = g(x) xác định trên R. Đặt S(x) = f(x) + g(x) và P(x) = f(x) g(x).

Xét các mệnh đề:

i) Nếu y = f(x) và y = g(x) là những hàm số chẵn thì y = S(x) và y = P(x) cũng là những hàm số chẵn

ii) Nếu y = f(x) và y = g(x) là những hàm số lẻ thì y = S(x) là hàm số lẻ và y = P(x) là hàm số chẵn

iii) Nếu y = f(x) là hàm số chẵn, y = g(x) là hàm số lẻ thì y = P(x) là hàm số lẻ

Số mệnh đề đúng là:

A. 1

B. 2

C. 3

D. Tất cả đều sai
#Toán lớp 10
1
CM
Cao Minh Tâm
29 tháng 9 2018

Đáp án C

Đúng(0)
PT
Pham Trong Bach
13 tháng 1 2017

Thế nào là một hàm số chẵn? Thế nào là một hàm số lẻ?
#Toán lớp 10
1
CM
Cao Minh Tâm
13 tháng 1 2017

– Hàm số y = f(x) có tập xác định D được gọi là hàm số chẵn nếu thỏa mãn hai điều kiện:

     + ∀ x ∈ D thì –x ∈ D

     + f(–x) = f(x).

– Hàm số y = f(x) có tập xác định D được gọi là hàm số lẻ nếu thỏa mãn hai điều kiện:

     + ∀ x ∈ D thì –x ∈ D

     + f(–x) = –f(x).

Đúng(0)
SG
Sách Giáo Khoa
29 tháng 3 2017

Thế nào là một hàm số chẵn ? Thế nào là một hàm số lẻ ?
#Toán lớp 10
1
Q
qwerty
30 tháng 3 2017

Cho hàm số y = f(x) có tập xác định D

Nếu \(\forall x\) ∈ D, ta có -x ∈ D và f(-x) = f(x) thì f(x) là hàm số chẵn trên D.

Nếu \(\forall x\) ∈ D, ta có -x ∈ D và f(-x) = -f(x) thì f(x) là hàm số lẻ trên D.

Đúng(0)
HM
Harvey Margaret
22 tháng 8 2021

Mệnh đề nào sau đây là sai?
A. Đồ thị hàm số chẵn nhận gốc tọa độ làm tâm đối xứng.
B. Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng.
C. Đồ thị hàm số lẻ nhận gốc tọa độ là tâm đối xứng.
D. Một hàm số không nhất thiết phải là hàm số chẵn hoặc hàm số lẻ
#Toán lớp 10
2
TA
Trần Ái Linh
22 tháng 8 2021

Mệnh đề nào sau đây là sai?
A. Đồ thị hàm số chẵn nhận gốc tọa độ làm tâm đối xứng.
B. Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng.
C. Đồ thị hàm số lẻ nhận gốc tọa độ là tâm đối xứng.
D. Một hàm số không nhất thiết phải là hàm số chẵn hoặc hàm số lẻ

Đúng(2)
NL
Nguyễn Lê Phước Thịnh
22 tháng 8 2021

Chọn A

Đúng(1)
DT
Dương Thanh Ngân
9 tháng 11 2021

xác định chẵn lẻ của hàm số |2x-3|+|2x+3|

xác định chẵn lẻ của hàm số \(\dfrac{x^3+x}{x^4+1}\)
#Toán lớp 10
1
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 11 2021

a.

\(D=R\)

\(f\left(-x\right)=\left|-2x-3\right|+\left|-2x+3\right|=\left|2x+3\right|+\left|2x-3\right|=f\left(x\right)\)

Hàm chẵn

b.

\(D=R\)

\(f\left(-x\right)=\dfrac{\left(-x\right)^3+\left(-x\right)}{\left(-x\right)^4+1}=\dfrac{-x^3-x}{x^4+1}=-\dfrac{x^3+x}{x^4+1}=-f\left(x\right)\)

Hàm lẻ

Đúng(0)
W
wfgwsf
31 tháng 10 2021

Hàm số f(x) = x (x4 - 3x2 -5) là :

A.Hàm số vừa chẵn, vừa lẻ           B.Hàm số chẵn

C.Hàm số không chẵn, không lẻ    D.Hàm số lẻ
#Toán lớp 10
1
NL
Nguyễn Lê Phước Thịnh
31 tháng 10 2021

Chọn D

Đúng(1)
W
wfgwsf
31 tháng 10 2021

Trong các hàm số sau đây: y = -|x|x2; y = x2 + 4|x|; y = -x4 + 2x2 có bao nhiêu hàm số chẵn?

A. Không có     B. Một hàm số chẵn    C. Hai hàm số chẵn               D. Ba hàm số chẵn
#Toán lớp 10
2
NL
Nguyễn Lê Phước Thịnh
31 tháng 10 2021

Chọn C

Đúng(0)
PD
Phí Đức
31 tháng 10 2021

=> D

Đúng(0)
W
wfgwsf
31 tháng 10 2021
Trong các hàm số sau đây: y = |x|x2; y = x4 + 4|x|; y = -7x4 + 2x2 có bao nhiêu hàm số chẵn?       A. Không có                    B. Một hàm số chẵn                                    C. Hai hàm số chẵn           D. Ba hàm số...
Đọc tiếp

Trong các hàm số sau đây: y = |x|x2; y = x4 + 4|x|; y = -7x4 + 2x2 có bao nhiêu hàm số chẵn?

       A. Không có                    B. Một hàm số chẵn                                    C. Hai hàm số chẵn           D. Ba hàm số chẵn.
#Toán lớp 10
0
PT
Pham Trong Bach
2 tháng 1 2018
Xét tính chẵn, lẻ của hai hàm số: f ( x ) = x + 2 - x - 2 ,   g ( x ) = - x A. f(x)  là hàm số chẵn, g(x)là hàm số chẵn. B. f(x) là hàm số lẻ,g(x) là hàm số chẵn. C. f(x)  là hàm số lẻ, g(x) là hàm số lẻ. D. f(x)  là hàm số chẵn, g(x) là hàm số...
Đọc tiếp

Xét tính chẵn, lẻ của hai hàm số: f ( x ) = x + 2 - x - 2 ,   g ( x ) = - x

A. f(x)  là hàm số chẵn, g(x)là hàm số chẵn.

B. f(x) là hàm số lẻ,g(x) là hàm số chẵn.

C. f(x)  là hàm số lẻ, g(x) là hàm số lẻ.

D. f(x)  là hàm số chẵn, g(x) là hàm số lẻ.
#Toán lớp 10
1
CM
Cao Minh Tâm
2 tháng 1 2018

Đáp án B

+ Hàm số f(x)  và g(x)  đều có tập xác định là D= R.

+ Xét hàm số y=f(x)  : Với mọi  và

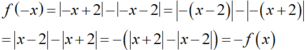
Nên y= f(x)  là hàm số lẻ.

+ Xét hàm số  y = g(x) :

 Với mọi  nên y = g(x)  là hàm số chẵn.

Chọn B.

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP