Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\left(a+b\right)^2=4ab\)<=> \(a^2+b^2+2ab=4ab\)
<=> \(a^2-2ab+b^2=0\)
<=> \(\left(a-b\right)^2=0\)=> a=b (đpcm)
b) Ta có: \(\left(a^2+b^2\right)\left(x^2+y^2\right)=\left(ax+by\right)^2\)
<=> \(a^2x^2+a^2y^2+b^2x^2+b^2y^2=a^2x^2+2axby+b^2y^2\)
<=> \(a^2y^2+b^2x^2-2axby=0\)
<=>\(\left(ay-bx\right)^2=0\)
<=>ay=bx(đpcm)
Chứng minh rằng
a/ (a+b)^2=(a-b)^2+4ab
b/ (a-b)^2=(a+b)^2-4ab
c/ (a^2+b^2)(x^2+y^2)=(ax-by)^2+(ay+bx)^2

a) \(\left(a+b\right)^2=a^2+2ab+b^2\left(1\right)\)
\(\left(a-b\right)^2+4ab=a^2-2ab+b^2+4ab=a^2-2ab+4ab+b^2=a^2+2ab+b^2\left(2\right)\)
Từ (1) và (2) => đpcm
b) \(\left(a-b\right)^2=a^2-2ab+b^2\left(3\right)\)
\(\left(a+b\right)^2-4ab=a^2+2ab+b^2-4ab=a^2+2ab-4ab+b^2=a^2-2ab+b^2\left(4\right)\)
Từ (3) và (4) =>đpcm
c) \(\left(a^2+b^2\right)\left(x^2+y^2\right)=a^2\left(x^2+y^2\right)+b^2\left(x^2+y^2\right)\)
\(=a^2x^2+a^2y^2+b^2x^2+b^2y^2\left(5\right)\)
\(\left(ax-by\right)^2+\left(ay+bx\right)^2=a^2x^2-2axby+b^2y^2+a^2y^2+2aybx+b^2x^2\)
\(=a^2x^2+a^2y^2+b^2x^2+b^2y^2\left(6\right)\)
Từ (5) và (6) =>đpcm

Ta có:
VT = (x2 + y2)(a2 + b2)
= x2a2 + x2b2 + y2a2 + y2b2
= (a2x2 + b2y2 + 2axby) + (a2y2 - 2aybx + b2x2)
= (ax + by)2 + (ay - bx)2
=> VT = VP => đpcm

Ta có : \(\left(a^2+b^2\right)\left(x^2+y^2\right)=\left(ax+by\right)^2\)
\(\Leftrightarrow a^2x^2+a^2y^2+b^2x^2+b^2y^2=a^2x^2+b^2y^2+2axby\)
\(\Leftrightarrow\left(ay\right)^2-2.ay.bx+\left(bx\right)^2=0\)
\(\Leftrightarrow\left(ay-bx\right)^2=0\Leftrightarrow ay-bx=0\)
Vậy ta có điều phải chứng minh.

Ta có: \(\left(ax+by\right)^2=\left(a^2+b^2\right)\left(x^2+y^2\right)\)
\(\Leftrightarrow a^2x^2+2abxy+b^2y^2=a^2x^2+a^2y^2+x^2b^2+b^2y^2\)
\(\Leftrightarrow2abxy=a^2y^2+x^2b^2\)
\(\Leftrightarrow\left(ay-xb\right)^2=0\)
\(\Leftrightarrow ay=xb\)
hay \(\dfrac{a}{x}=\dfrac{b}{y}\)

\(\left(a^2+b^2\right)\left(x^2+y^2\right)=\left(ax+by\right)^2\)
\(\Leftrightarrow\) \(\dfrac{a}{x}=\dfrac{b}{y}\)
\(\Leftrightarrow ay=bx\)
\(\Leftrightarrow ay-bx=0\)
( Bất đẳng thức Bu - nhi - a - cốp - xki )


a)
\(A=-\left(a-b^2\right)+b\)
\(=>2X\left(x^2+b\right)\)
Chứng minh
A=min a2 + b =........
Câu b tương tự
a) \(2.\left(a^2+b^2\right)=\left(a+b\right)^2\Leftrightarrow2.\left(a^2+b^2\right)-\left(a+b\right)^2=0\)
\(\Leftrightarrow a^2-2ab+b^2=0\Leftrightarrow\left(a-b\right)^2=0\Leftrightarrow a-b=0\Leftrightarrow a=b\)

\(\left(a^2+b^2\right)\left(x^2+y^2\right)=a^2x^2+a^2y^2+b^2x^2+b^2y^2\)
\(=\left(a^2x^2-2axby+b^2y^2\right)+\left(a^2y^2+2axby+b^2x^2\right)\)
\(=\left(ax-by\right)^2+\left(ay+bx\right)^2\)
Cái này trong SGK nè
BĐVT ta có:
\(\left(a^2+b^2\right)\left(x^2+y^2\right)=a^2x^2+a^2y^2+b^2x^2+b^2y^2\)(1)
BĐVP ta có:
\(\left(ax-by\right)^2+\left(ay+bx\right)^2=a^2x^2+a^2y^2-2abxy+2abxy+b^2x^2+b^2y^2=a^2x^2+a^2y^2+b^2x^2+b^2y^2\left(2\right)\)
Từ (1) và (2) suy ra:( a2 + b2 ).( x2 + y2) = ( ax - by)2 + ( ay + bx)2
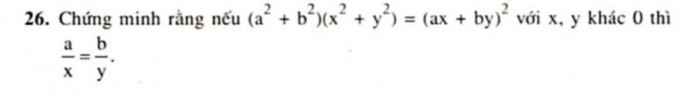
a) VP=(a-b)2+4ab
=a2-2ab+b2+4ab
=a2+b2+2ab
=(a+b)2=VT
Vậy (a+b)^2 = (a-b)^2 +4ab
b) VP=(a+b)2-4ab
=a2+2ab+b2-4ab
=a2-2ab+b2
=(a-b)2=VT
Vậy (a-b)^2 = (a+b)^2 - 4ab
c)
VP=(ax-by)2+(ay+bx)2
=a2x2-2axby+b2y2+a2y2+2axby+b2x2
=a2x2+b2y2+a2y2+b2x2
=(a2x2+b2x2)+(b2y2+a2y2)
=x2.(a2+b2)+y2.(a2+b2)
=(a2+b2)(a2+y2)=VT
Vậy ( a^2 + b^2 ).(x^2 +y^2) = (ax - by)^2 +(ay+bx)^2