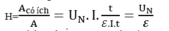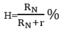K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 8 2023
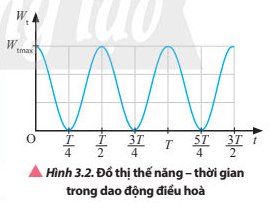
Thế năng của vật đạt giá trị lớn khi ở vị trí hai biên và đạt giá trị nhỏ nhất ở vị trí cân bằng khi vật di chuyển từ vị trí biên đến vị trí cân bằng thế năng của vật giảm dần từ giá trị lớn nhất về 0 và ngược lại.
H9
HT.Phong (9A5)
CTVHS
18 tháng 8 2023
Nhiệt lượng của đoạn mạch tỏa ra khi có dòng điện chạy qua là: Q=UIt
Mà: \(R=\dfrac{U}{I}\Rightarrow Q=I^2Rt=\dfrac{U^2}{R}\cdot t\)
HQ
Hà Quang Minh
Giáo viên
5 tháng 11 2023
Ta có:
\(W_t=\dfrac{1}{2}m\omega^2A^2cos^2\left(\omega t+\varphi_0\right)\\ W_d=\dfrac{1}{2}mv^2=\dfrac{1}{2}m\omega^2A^2sin^2\left(\omega t+\varphi_0\right)\\ \Rightarrow W=W_t+W_d=\dfrac{1}{2}m\omega^2A^2\left[cos^2\left(\omega t+\varphi_0\right)+sin^2\left(\omega t+\varphi_0\right)\right]\\ \Rightarrow W=\dfrac{1}{2}m\omega^2A^2\)
VT
4 tháng 9 2018
Nếu mạch ngoài chỉ có điện trở thuần:
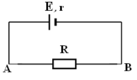
Ta có: UN = I.RN và E = I.(RN + r)
Hiệu suất của nguồn điện khi này:
VT
26 tháng 4 2019
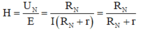
Giải thích: Đáp án C
+ Công suất không được tính bằng biểu thức P = 0,5I2R.
HQ
Hà Quang Minh
Giáo viên
27 tháng 8 2023
Biểu thức liên hệ là \(R=\dfrac{U}{I}\) \(\Rightarrow I=\dfrac{U}{R}\)
Với R là hằng số, cường độ dòng điện I có dạng \(I=aU\left(a=\dfrac{1}{R}\right)\) là hàm số bậc nhất của U. Do đó, đồ thị I – U là một đoạn thẳng.
HQ
Hà Quang Minh
Giáo viên
5 tháng 11 2023
Ta có: I = Snve
U = E.l
\(\rho = \frac{E}{J} = \frac{{ES}}{I} = \frac{{ES}}{{Snve}} = \frac{E}{{nve}}\) với J là mật độ dòng điện J = \(\frac{I}{S}\)(A/m2)
Từ R = \(\frac{U}{I}\) ⇒ R = \(\frac{{E.l}}{{Snve}} = \rho \frac{l}{S}\)