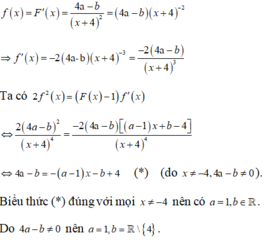Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Đề bài em ghi sai thì phải
Vì:
\(x+y=2\left(\sqrt{x-3}+\sqrt{y-3}\right)\)
\(\Leftrightarrow\left(x-3-2\sqrt{x-3}+1\right)+\left(y-3-2\sqrt{y-3}+1\right)+4=0\)
\(\Leftrightarrow\left(\sqrt{x-3}-1\right)^2+\left(\sqrt{y-3}-1\right)^2+4=0\) (vô lý)
b.
Xét hàm \(f\left(x\right)=x^3+ax^2+bx+c\)
Hàm đã cho là hàm đa thức nên liên tục trên mọi khoảng trên R
Hàm bậc 3 nên có tối đa 3 nghiệm
\(f\left(-2\right)=-8+4a-2b+c>0\)
\(f\left(2\right)=8+4a+2b+c< 0\)
\(\Rightarrow f\left(-2\right).f\left(2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc (-2;2)
\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=x^3\left(1+\dfrac{a}{x}+\dfrac{b}{x^2}+\dfrac{c}{x^3}\right)=+\infty.\left(1+0+0+0\right)=+\infty\)
\(\Rightarrow\) Luôn tồn tại 1 số thực dương n đủ lớn sao cho \(f\left(n\right)>0\)
\(\Rightarrow f\left(2\right).f\left(n\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(2;n\right)\) hay \(\left(2;+\infty\right)\)
Tương tự \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=-\infty\Rightarrow f\left(-2\right).f\left(m\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-\infty;-2\right)\)
\(\Rightarrow f\left(x\right)\) có đúng 3 nghiệm pb \(\Rightarrow\) hàm cắt Ox tại 3 điểm pb

Chọn D
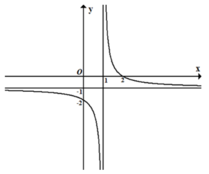
Từ đồ thị hàm số, ta suy ra
Đồ thị hàm số có tiệm cận đứng là đường thẳng x = 1, tiệm cận ngang là đường thẳng y = -1
Đồ thị hàm số đi qua các điểm A(2;0), B(0;-2)
Từ biểu thức hàm số y = a x + b x + c (vì đồ thị hàm số là đồ thị hàm nhất biến nên ac - b ≠ 0), ta suy ra
Đồ thị hàm số có tiệm cận đứng là đường thẳng x = -c, tiệm cận ngang là đường thẳng y = a.
Đồ thị hàm số đi qua ![]()
Đối chiếu lại, ta suy ra c = -1, a = -1, b
Vậy ![]()

a) Xét hàm số f(x) = tanx − sinx trên nửa khoảng [0; π/2);

x ∈ [0;1/2)
Dấu “=” xảy ra khi x = 0.
Suy ra f(x) đồng biến trên nửa khoảng [0; π/2)
Mặt khác, ta có f(0) = 0, nên f(x) = tanx – sinx > 0 hay tanx > sinx với mọi x ∈ [0; 1/2)
b) Xét hàm số h(x) trên [0; + ∞ )
![]()
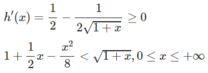
Dấu “=” xẩy ra chỉ tại x = 0 nên h(x) đồng biến trên nửa khoảng [0; + ∞ ).
Vì h(x) = 0 nên
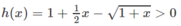
Hay
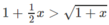
Xét hàm số trên f(x) trên [0; + ∞ );
![]()
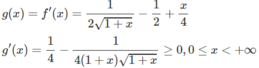
Vì g(0) = 0 và g(x) đồng biến trên nửa khoảng [0; + ∞ ) nên g(x) ≥ 0, tức là f′(x) ≥ 0 trên khoảng đó và vì dấu “=” xảy ra chỉ tại x = 0 nên f(x) đồng biến trên nửa khoảng .
Mặt khác, ta có f(0) = 0 nên
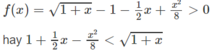
Với mọi 0 < x < + ∞ .

\(\sqrt{1+\dfrac{1}{x^2}+\dfrac{1}{\left(x+1\right)^2}}=\sqrt{\dfrac{x^2+\left(x+1\right)^2+x^2\left(x+1\right)^2}{x^2\left(x+1\right)^2}}=\sqrt{\dfrac{x^2\left(x+1\right)^2+2x^2+2x+1}{x^2\left(x+1\right)^2}}\)
\(=\sqrt{\dfrac{\left(x^2+x\right)^2+2\left(x^2+x\right)+1}{\left(x^2+x\right)^2}}=\sqrt{\dfrac{\left(x^2+x+1\right)^2}{\left(x^2+x\right)^2}}=\dfrac{x^2+x+1}{x^2+x}\)
\(=1+\dfrac{1}{x}-\dfrac{1}{x+1}\)
\(\Rightarrow f\left(1\right).f\left(2\right)...f\left(2020\right)=5^{1+1-\dfrac{1}{2}+1+\dfrac{1}{2}-\dfrac{1}{3}+...+1+\dfrac{1}{2020}-\dfrac{1}{2021}}\)
\(=5^{2021-\dfrac{1}{2021}}\)
\(\Rightarrow\dfrac{m}{n}=2021-\dfrac{1}{2021}=\dfrac{2021^2-1}{2021}\)
\(\Rightarrow m-n^2=2021^2-1-2021^2=-1\)

1.\(\dfrac{log_ac}{log_{ab}c}=log_ac.log_c\left(ab\right)=log_ac.\left(log_ca+log_cb\right)=log_ac.log_ca+log_ac.log_cb=\dfrac{log_ac}{log_ac}+\dfrac{log_cb}{log_ca}=1+log_ab\)
2. \(log_{ax}bx=\dfrac{log_abx}{log_aax}=\dfrac{log_ab+log_ax}{log_aa+log_ax}=\dfrac{log_ab+log_ax}{1+log_ax}\)
3. \(\dfrac{1}{log_ax}+\dfrac{1}{log_{a^2}x}+...+\dfrac{1}{log_{a^n}x}=log_xa+log_xa^2+...+log_xa^n\)
\(=log_xa+2log_xa+...+n.log_xa=log_xa+2log_xa+...+n.log_xa\)
\(=log_xa.\left(1+2+...+n\right)=\dfrac{n\left(n+1\right)}{2}log_xa=\dfrac{n\left(n+1\right)}{2.log_ax}\)