K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
1 tháng 1 2022
a thuộc N nên a có dạng 5k,5k+1,5k+2,5k+3,5k+4
với a=5k thì a^2 và a chia hết cho 5 mà 2021 ko chia hết nên tổng ko chia hết
với a=5k+1 =>a2+a+2021=(5k+1)2+5k+1+2021=25k2+15k+2023 không chia hết cho 5
bạn làm tương tự với mấy cây còn lại, ko đc thì nói nhé
chúc bạn học tốt
NNBC-1/1/2022
HP
1
TV
1
DD
Đoàn Đức Hà
Giáo viên
18 tháng 3 2022
Ta có: \(\frac{2022}{2021^2+k}\le\frac{2022}{2021^2}\) (với \(k\)là số tự nhiên bất kì)
Ta có:
\(A=\frac{2022}{2021^2+1}+\frac{2022}{2021^2+2}+...+\frac{2022}{2021^2+2021}\)
\(\le\frac{2022}{2021^2}+\frac{2022}{2021^2}+...+\frac{2022}{2021^2}=\frac{2022}{2021^2}.2021=\frac{2022}{2021}\)
Ta có: \(\frac{2022}{2021^2+k}>\frac{2022}{2021^2+2021}=\frac{2022}{2021.2022}=\frac{1}{2021}\)với \(k\)tự nhiên, \(k< 2021\))
Suy ra \(A=\frac{2022}{2021^2+1}+\frac{2022}{2021^2+2}+...+\frac{2022}{2021^2+2021}\)
\(>\frac{1}{2021}+\frac{1}{2021}+...+\frac{1}{2021}=\frac{2021}{2021}=1\)
Suy ra \(1< A\le\frac{2022}{2021}\)do đó \(A\)không phải là số tự nhiên.
11 tháng 2 2020
Giả sử: a ≥ b thì
a là bội của b nên a =b.k (k ∈ Z, k ≠ 0)
b là bội của a nên b = a.q (q ∈ Z, q ≠ 0, q ≥ k )
Thay b = a.q thì:
a = b.k = a.q.k
⇒q.k = 1
⇒k ∈ Ư (1) (k,q ∈ Z;k,q ≠ 0)
Mà q ≥ k
⇒k = 1,q = −1;k = q = 1
Nếu q = 1; k= -1 thì b.k = b.(-1) = -b
Nếu q = 1; k= 1 thì b.k = b.1 = b,đpcm
14 tháng 10 2021
\(10^{2021}+8=1....0+8⋮9\) (vì có tổng các chữ số là 9 chia hết cho 9)
\(10^{2021}+8=....00+8=....008⋮8\) (vì có 3 chữ số tận cùng là 008 chia hết cho 8)
Mà \(\left(8;9\right)=1\) nên \(10^{2021}+8⋮72\) hay là bội của 72
BT
1
NM
Nguyễn Minh Quang
Giáo viên
13 tháng 10 2021
ta có a+2021 và a+2020 là hai số tự nhiên liên tiếp
nên chắc chắc có 1 số chẵn trong hai số đó
vậy tích (a+2021)(a+2020) là số chẵn, hay là bội của 2
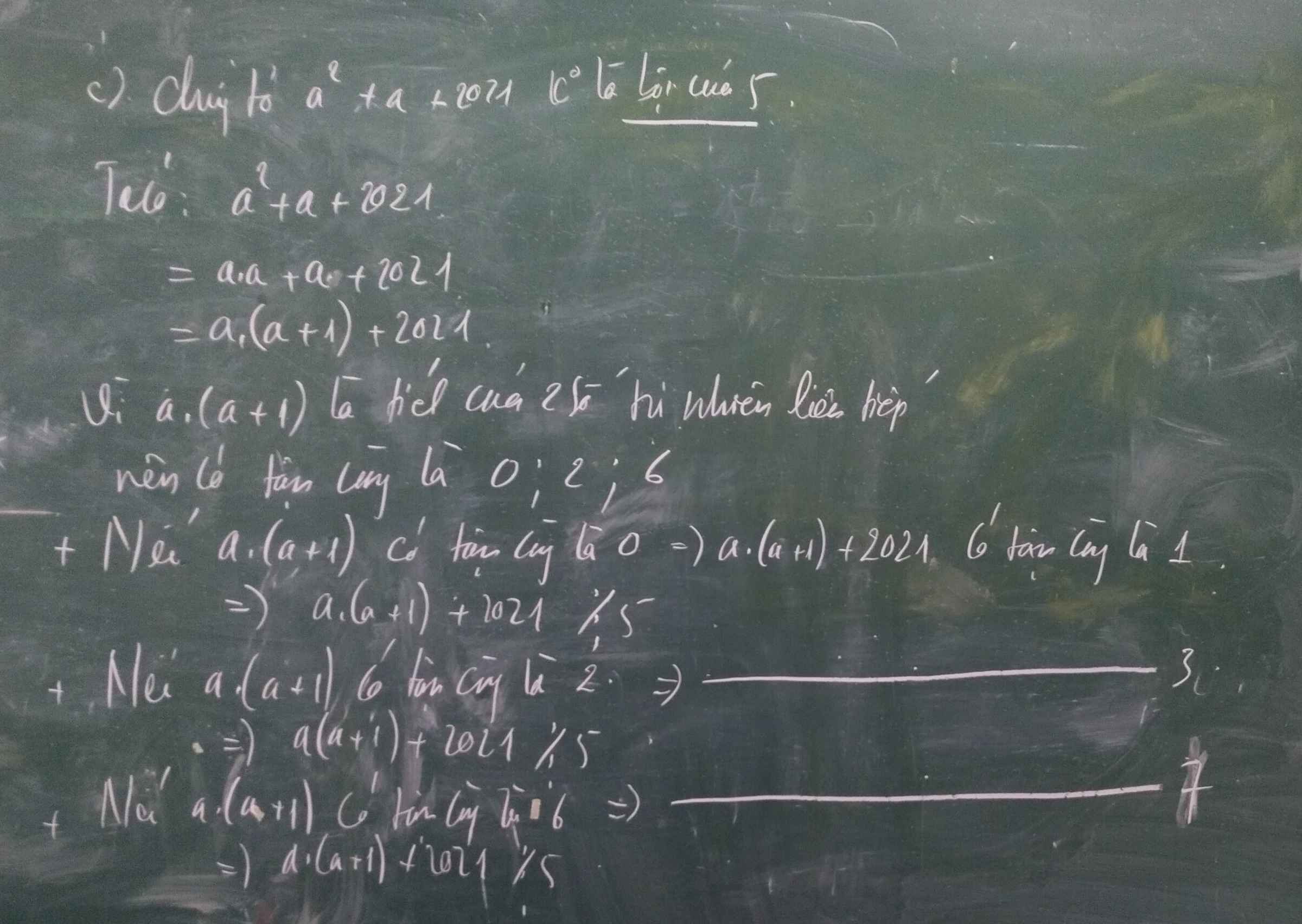
Ta có :
a²+a+2021
= a.a+a+2021
= a.(a+1)+2021
Ví a.(a+1) là tích hai số liên tiếp nên có tân cùng là 0;1;2;6
⇒ a.(a+1)+2021 có tân cùng là 1;2;3;7 và không chia hết cho 5
Vậy a²+a+2021 không chia hết cho 5