Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác AMN có góc MAN = 1200 suy ra tam giác AMN cân tại A
suy ra góc AMN=góc ANM = 300
Xét tam giác AHM và tam giác AHN
có AH chung
góc AHM = góc AHN = 900
AM=AN (vì tam giác AMN cân tại A)
suy ra tam giác AHM = tam giác AHN ( cạnh huyền-cạnh góc vuông)
suy ra góc MAH=góc HAN (hai góc tương ứng)
suy ra AH là tia phân giác của góc MAN
b) Xét tam giác vuong AHD và tam giác vuông AhE
có AH chung
góc hAD=góc HAE (CMT)
suy ra tam giác AHD = tam giác AHE ( cạnh huyền-góc nhọn) (1)
suy ra AD=AE suy ra tam giác ADE cân tại A
suy ra góc ADE=góc AED=300
suy ra góc ADE = góc AMN = 300
mà góc ADE đồng vị với góc AMN
suy ra DE//MN
c) tam giác HEN vuông tại E suy ra góc EHN = 600
tam giác HDM vuông tại D suy ra góc DHM = 600
mà góc DHM + góc DHE + góc EHN = 1800
suy ra góc DHE = 600 (2)
Từ (1) suy ra DH = HE suy ra tam giác DHE cân tại H (3)
Từ (2) và (3) suy ra tam giác DHE đều
d) Xét tam giác MIN vuoog tại N suy ra góc NIM = 600
góc IAN kề bù với góc NAM
suy ra góc NAI = 600
tam giác ANI có góc AIN=góc ANI=góc IAN = 600
suy ra tam giác ANI đều
suy ra AI = NI = 10cm

Xét tam giác AMN có góc MAN = 1200 suy ra tam giác AMN cân tại A
suy ra góc AMN=góc ANM = 300
Xét tam giác AHM và tam giác AHN
có AH chung
góc AHM = góc AHN = 900
AM=AN (vì tam giác AMN cân tại A)
suy ra tam giác AHM = tam giác AHN ( cạnh huyền-cạnh góc vuông)
suy ra góc MAH=góc HAN (hai góc tương ứng)
suy ra AH là tia phân giác của góc MAN
b) Xét tam giác vuong AHD và tam giác vuông AhE
có AH chung
góc hAD=góc HAE (CMT)
suy ra tam giác AHD = tam giác AHE ( cạnh huyền-góc nhọn) (1)
suy ra AD=AE suy ra tam giác ADE cân tại A
suy ra góc ADE=góc AED=300
suy ra góc ADE = góc AMN = 300
mà góc ADE đồng vị với góc AMN
suy ra DE//MN
c) tam giác HEN vuông tại E suy ra góc EHN = 600
tam giác HDM vuông tại D suy ra góc DHM = 600
mà góc DHM + góc DHE + góc EHN = 1800
suy ra góc DHE = 600 (2)
Từ (1) suy ra DH = HE suy ra tam giác DHE cân tại H (3)
Từ (2) và (3) suy ra tam giác DHE đều
d) Xét tam giác MIN vuoog tại N suy ra góc NIM = 600
góc IAN kề bù với góc NAM
suy ra góc NAI = 600
tam giác ANI có góc AIN=góc ANI=góc IAN = 600
suy ra tam giác ANI đều
suy ra AI = NI = 10cm

tu ve hinh :
xet tamgiac AMN can tai A (gt) => goc AMN = goc ANM va AM = AN (dn)
AH vuong goc voi MN => goc AHN = goc AHM = 90o (dn)
=> tamgiac AMH = tamgiac ANH (ch - gn)
=> goc NAH = goc MAH (dn) ma AH nam giua AN va AM
=> AH la phan giac cua goc MAN

Bạn tự vẽ hình nha
a.Vì tam giác ABC cân tại A nên AB= AC và góc ABC = góc ACB
<=> góc ABM = góc ACN (vì các góc kề bù với nhau)
Xét tam giác ABM và tam giác ACN
Có: AB = AC (CMT)
góc ABM = góc ACN (CMT)
BM = CN (gt)
<=> tam giác ABM = tam giác ACN (c.g.c)
<=> AM = AN ( 2 góc tương ứng)
<=> tam giác AMN cân tại A
b. Vì tam giác ABM = tam giác ACN (CMT)
<=> góc MAB = góc CAN ( 2 góc tương ứng)
Xét tam giác vuông AHB và tam giác vuông AKC
Có: AB= AC (CMT)
góc AHB= góc AKC= 90 độ
góc MAB = góc CAN (CMT)
<=> tam giác AHB = tam giác AKC ( cạnh huyền- góc nhọn)

a) Xét tam giác ABD và tam giác HBD có :
góc ABD = góc HBD (BD là tia pg)
góc BAD = góc BHD=90 độ (gt)
BD là cạnh chung
=> Tam giác ABD = Tam giác HBD (CH-GN)
=> AD = DH ( 2 cạnh tương ứng )
b) Xét tam giác DHC có :
Góc DHC = 90 độ => DC là cạnh huyền => DC > DH
Ta lại có : AD=DH ( cm ở câu a )
=> DC>AD

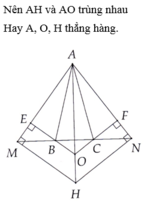
a/
Ta có
\(\widehat{ABC}=\widehat{ACB}\) (2 góc ở đáy của tg cân ABC) (1)
\(\widehat{ABM}+\widehat{ABC}=\widehat{ACN}+\widehat{ACB}=180^o\)(2)
Từ (1) và (2) \(\Rightarrow\widehat{ABM}=\widehat{ACN}\)
Xét \(\Delta ABM\) và \(\Delta ACN\) có
AB=AC (cạnh bên của tg cân ABC)
BM=CN (gt)
\(\widehat{ABM}=\widehat{ACN}\left(cmt\right)\)
\(\Rightarrow\Delta ABM=\Delta ACN\left(c.g.c\right)\Rightarrow AM=AN\Rightarrow\Delta AMN\)cân tại A
b/
Xét tg vuông BME và tg vuông CNF có
\(\widehat{ABM}=\widehat{ACN}\left(cmt\right)\Rightarrow\widehat{AMN}=\widehat{ANM}\) (2 góc ở đáy của tg cân AMN)
BM=CN (gt)
\(\Rightarrow\Delta BME=\Delta CNF\) (Hai tg vuông có cạnh huyền và một góc nhọn tương ứng = nhau thì bằng nhau)
c/
Xét tg cân AMN có AM=AN (1)
\(\Delta BME=\Delta CNF\left(cmt\right)\Rightarrow ME=NF\) (2)
Từ (1) và (2) => AM-ME=AN-NF => AE=AF
Xét tg vuông AEO và tg vuông AFO có
AE=AF (cmt)
AO chung
\(\Rightarrow\Delta AEO=\Delta AFO\) (Hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau thì bằng nhau)
\(\Rightarrow\widehat{OAE}=\widehat{OAF}\) => AO là phân giác của \(\widehat{MAN}\)
d/
Ta có
\(\widehat{HMN}=\widehat{HMA}-\widehat{AMN}=90^o-\widehat{AMN}\)
\(\widehat{HNM}=\widehat{HNA}-\widehat{ANM}=90^o-\widehat{ANM}\)
Mà \(\widehat{AMN}=\widehat{ANM}\)
\(\Rightarrow\widehat{HMN}=\widehat{HNM}\Rightarrow\Delta HMN\) cân tại H
Ta có
\(OE\perp AM;HM\perp AM\)=> OE//HM \(\Rightarrow\widehat{AOE}=\widehat{AHM}\) (góc đồng vị)
Chứng minh tương tự ta cũng có OF//HN \(\Rightarrow\widehat{AOF}=\widehat{AHN}\) (góc đồng vị)
Mà \(\Delta AEO=\Delta AFO\Rightarrow\widehat{AOE}=\widehat{AF}\)
\(\Rightarrow\widehat{AHM}=\widehat{AHN}\)=> HO là phân giác của \(\widehat{MHN}\)
Xét tg cân HMN có
HO là phân giác của \(\widehat{MHN}\)=> HO là đường trung trực của tg HMN (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường trung trực) => \(HO\perp MN\) tại trung điểm của MN
Xét tg cân AMN có
AO là đường phân giác của \(\widehat{MAN}\) (cmt) => AO là đường trung trực của tg AMN (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường trung trực) => \(AO\perp MN\) tại trung điểm của MN
=> AO trung HO (Từ 1 điểm trên đường thẳng chỉ duy nhất dựng được 1 đường thẳng vuông góc với đường thẳng đã cho)
=> A; O; H thẳng hàng

a) Xét t/giác AMH và t/giác ANH
có: AM = AN (gt)
\(\widehat{M}=\widehat{N}\)(gt)
\(\widehat{AHM}=\widehat{AHN}=90^0\)(gt)
=> t/giác AMH = t/giác ANH (ch - gn)
=> \(\widehat{MAH}=\widehat{NAH}\) (2 góc t/ứng)
=> AH là tia p/giác của góc MAN
b) Xét t/giác ADH và t/giác AEH
có: AH : chung
\(\widehat{DAH}=\widehat{EAH}\) (cmt)
\(\widehat{ADH}=\widehat{AEH}=90^0\)(gt)
=> t/giác ADH = t/giác AEH (ch.gn)
=> AD = AE( 2 cạnh t/ứng)
=> t/giác ADE cân tại A
a) Xét \(\Delta AHM\)và \(\Delta AHN\)có:
\(AM=AN\)( \(\Delta AMN\)cân tại A )
AH là cạnh chung
\(\widehat{AHM}=\widehat{AHN}\left(=90^0\right)\)
\(\Rightarrow\Delta AHM=\Delta AHN\left(ch.gn\right)\)
\(\Rightarrow\widehat{A_1}=\widehat{A_2}\)( 2 góc tương ứng )
=> AH là tia phân giác \(\widehat{MAN}\)( đpcm )