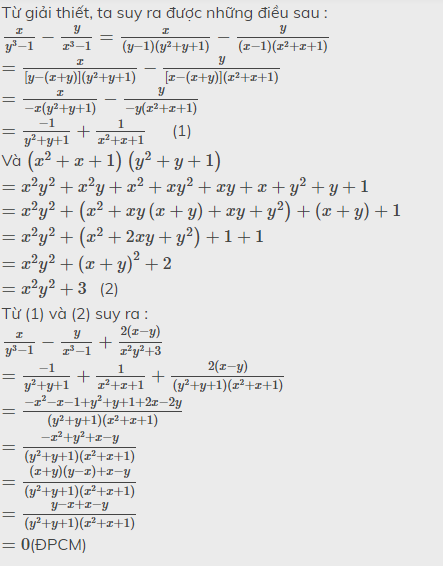NG
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HG
0
DN
1
NM
Nguyễn Minh Quang
Giáo viên
6 tháng 1 2021
Xét \(\frac{x}{y^3-1}+\frac{y}{x^3-1}=\frac{1-y}{y^3-1}+\frac{1-x}{x^3-1}=-\frac{1}{x^2+x+1}-\frac{1}{y^2+y+1}\)
\(=-\frac{x^2+y^2+x+y+2}{\left(x^2+x+1\right)\left(y^2+y+1\right)}=-\frac{x^2+y^2+3}{x^2y^2+xy\left(x+y\right)+x^2+y^2+xy+x+y+1}\)
\(=-\frac{\left(x+y\right)^2-2xy+3}{x^2y^2+x^2+y^2+2xy+2}=-\frac{4-2xy}{x^2y^2+3}=\frac{2\left(xy-2\right)}{x^2y^2+3}\)
từ đó ta có đpcm
DT
0
TT
2
MN
29 tháng 3 2020
Từ giải thiết, ta suy ra được những điều sau :
\(\frac{x}{y^3-1}-\frac{y}{x^3-1}=\frac{x}{\left(y-1\right)\left(y^2+y+1\right)}-\frac{y}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\frac{x}{\left[y-\left(x+y\right)\right]\left(y^2+y+1\right)}-\frac{y}{\left[x-\left(x+y\right)\right]\left(x^2+x+1\right)}\)
\(=\frac{x}{-x\left(y^2+y+1\right)}-\frac{y}{-y\left(x^2+x+1\right)}\)
\(=\frac{-1}{y^2+y+1}+\frac{1}{x^2+x+1}\) (1)
Và \(\left(x^2+x+1\right)\left(y^2+y+1\right)\)
\(=x^2y^2+x^2y+x^2+xy^2+xy+x+y^2+y+1\)
\(=x^2y^2+\left(x^2+xy\left(x+y\right)+xy+y^2\right)+\left(x+y\right)+1\)
\(=x^2y^2+\left(x^2+2xy+y^2\right)+1+1\)
\(=x^2y^2+\left(x+y\right)^2+2\)
\(=x^2y^2+3\) (2)
Từ (1) và (2) suy ra :
\(\frac{x}{y^3-1}-\frac{y}{x^3-1}+\frac{2\left(x-y\right)}{x^2y^2+3}\)
\(=\frac{-1}{y^2+y+1}+\frac{1}{x^2+x+1}+\frac{2\left(x-y\right)}{\left(y^2+y+1\right)\left(x^2+x+1\right)}\)
\(=\frac{-x^2-x-1+y^2+y+1+2x-2y}{\left(y^2+y+1\right)\left(x^2+x+1\right)}\)
\(=\frac{-x^2+y^2+x-y}{\left(y^2+y+1\right)\left(x^2+x+1\right)}\)
\(=\frac{\left(x+y\right)\left(y-x\right)+x-y}{\left(y^2+y+1\right)\left(x^2+x+1\right)}\)
\(=\frac{y-x+x-y}{\left(y^2+y+1\right)\left(x^2+x+1\right)}\)
\(=0\)(ĐPCM)
7 tháng 4 2020
Biến đổi
\(\frac{x}{y^3-1}-\frac{y}{x^3-1}=\frac{x^4-x-y^4+y}{\left(x^3-1\right)\left(y^3-1\right)}=\frac{\left(x^4-y^4\right)-\left(x-y\right)}{xy\left(y^2+y+1\right)\left(x^2+x+1\right)}\)
(do x+y=1 => y-1=-x và x-1=-y)
\(=\frac{\left(x-y\right)\left(x+y\right)\left(x^3+y^3\right)-\left(x-y\right)}{xy\left(x^2y^2+y^2x+y^2+yx^2+xy+y+x^2+x+1\right)}\)
\(=\frac{\left(x-y\right)\left(x^2+y^2-1\right)}{xy\left[x^2y^2+xy\left(x+y\right)+x^2+y^2+xy+2\right]}\)
\(=\frac{\left(x-y\right)\left(x^2-x+y^2-y\right)}{xy\left[x^2y^2+\left(x+y\right)^2+2\right]}=\frac{\left(x-y\right)\left[x\left(x-1\right)+y\left(y-1\right)\right]}{xy\left(x^2y^2+3\right)}\)
\(=\frac{\left(x-y\right)\left[x\left(-y\right)+y\left(-x\right)\right]}{xy\left(x^2y^2+3\right)}=\frac{\left(x-y\right)\left(-2xy\right)}{xy\left(x^2y^2+1\right)}=\frac{-2\left(x-y\right)}{x^2y^2+3}\)
=> ĐPCM