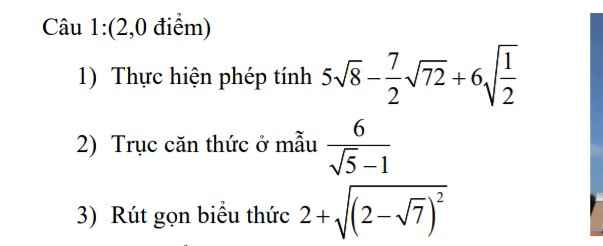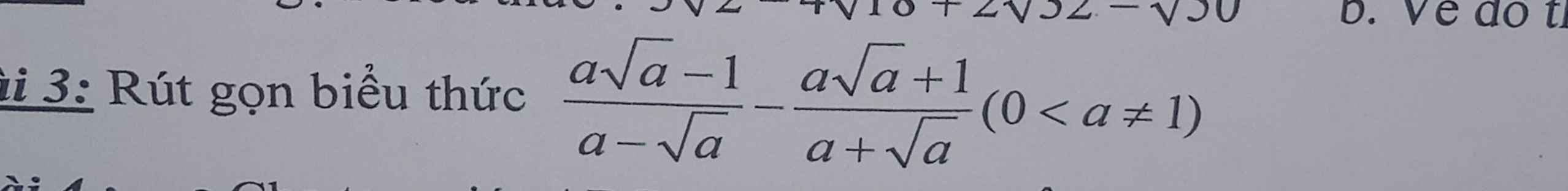Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Xét (O) có
ΔABC nội tiếp đường tròn
AB là đường kính
Do đó: ΔBAC vuông tại C

\(1,=10\sqrt{2}-21\sqrt{2}+3\sqrt{2}=-8\sqrt{2}\\ 2,=\dfrac{6\left(\sqrt{5}+1\right)}{4}=\dfrac{3\sqrt{5}+3}{2}\\ 3,=2+\left|2-\sqrt{7}\right|=2+\sqrt{7}-2=\sqrt{7}\)

bạn đăng tách ra để mn cùng giúp nhé
Bài 1 :
a. (d) // (d') <=> \(\left\{{}\begin{matrix}m^2-2=-1\\3\ne m+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2=1\\m\ne1\end{matrix}\right.\Leftrightarrow m=-1\)
b, Hoành độ giao điểm (d1) ; (d2) tm pt
\(2x+1=x+2\Leftrightarrow x=1\)
=> y = 3
Vậy (d1) cắt (d2) tại A(1;3)
Để 3 đường đồng quy khi (d3) đi qua A(1;3)
hay A(1;3) thuộc (d3)
<=> \(m^2+2-2m+1=3\Leftrightarrow m^2-2m=0\Leftrightarrow m=0;m=2\)


để nhận được câu trả lời nhanh và chi tiết thì bạn vui lòng chia nhỏ ra để đăng nhé! Mỗi lần chỉ nên đăng 1 - 2 câu thôi!

a: Xét ΔABH vuông tại H có HF là đường cao ứng với cạnh huyền AB
nên \(AF\cdot AB=AH^2\left(1\right)\)
Xét ΔACH vuông tại H có HE là đường cao ứng với cạnh huyền AC
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)

x,y là số nguyên tố đúng ko? bn có nhiueeuf câu hỏi nên mik trả lời nhầm.(ko phait thì thui nhé)
\(\left(3x^2+6x+3\right)+\left(3y^2+3y+1\right)+y^2-8=0\)
\(\Leftrightarrow3\left(x+1\right)^2+3\left(y+\frac{1}{2}\right)^2-\frac{9}{4}-8=0\)
\(\Leftrightarrow12\left(x+1\right)^2+3\left(y+1\right)^2=41\)
\(\Rightarrow12\left(x+1\right)^2\le41\Rightarrow\left(x+1\right)^2\le3\Rightarrow x+1\in\left\{1;0;-1\right\}\Rightarrow x\in\left\{0;-1;-2\right\}\)
Bạn làm nốt

\(=\dfrac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}+1\right)}\)
\(=\dfrac{a+\sqrt{a}+1-a+\sqrt{a}-1}{\sqrt{a}}=\dfrac{2\sqrt{a}}{\sqrt{a}}=2\)